Stochastic economic sizing and placement of renewable integrated energy system with combined hydrogen and power technology in the active distribution network
November 16, 2024
Abstract
The current study concentrates on the planning (sitting and sizing) of a renewable integrated energy system that incorporates power-to-hydrogen (P2H) and hydrogen-to-power (H2P) technologies within an active distribution network. This is expressed in the form of an optimization model, in which the objective function is to reduce the annual costs of construction and maintenance of integrated energy systems. The model takes into account the planning and operation model of wind, solar, and bio-waste resources, as well as hydrogen storage (a combination of P2H, H2P, and hydrogen tank), and the optimal power flow constraints of the distribution network. Electrical and hydrogen energy are administered in an integrated energy system. The modeling of the uncertainties regarding the quantity of load and renewable resources is achieved through stochastic optimization using the Unscented Transformation method. The novelties of the scheme include the sizing and placement of a combined hydrogen and power-based renewable integrated energy system, the consideration of the impacts of bio-waste units, P2H, and H2P systems on the planning of the integrated energy system and the operation of the active distribution network, and the modeling of uncertainties using the Unscented Transformation method to reduce the calculation time. The study’s results demonstrate the scheme’s ability to improve the technical conditions of the distribution network by considering the optimal planning of integrated energy systems. In comparison to the network power flow, the operation status of the network has been improved by approximately 23-45% through the optimal siting, sizing, and energy management of hydrogen storage equipment, as well as renewable resources in the form of integrated energy systems. In other words, optimal energy management and planning of the integrated energy systems in the distribution network has been able to reduce energy losses and voltage drop by 44.5% and 42.4% compared to the load flow studies. In this situation, peak load carrying capability has increased by about 23.7%. In addition, compared to the case of the network with renewable resources, the overvoltage has decreased by about 43.5%. Also, Unscented Transformation method has a lower calculation time than scenario-based stochastic optimization.
Introduction
Motivation
Integrated energy systems (IESs) are a method of aggregating and coordinating energy consumption management programs, storage, and resources1. Renewable energy sources, which are environmentally favorable, are typically implemented in an IES to mitigate emissions. These resources are available in a variety of forms, including tidal units (TU), photovoltaic (PV), wind systems (WS), and bio-waste systems (BS)2. Their generation capacity is unpredictable and fluctuates2. Consequently, the utilization of storage devices in IES is regarded as a sustainable energy source3. Storage devices can be implemented to optimize energy management in IES, in addition to compensating for the power fluctuations of renewable sources. Various varieties of storage devices exist. One such variety is hydrogen storage, which is equipped with hydrogen-to-power (H2P) and power-to-hydrogen (P2H) technologies. In addition to its capacity to store electrical energy, this storage system can also be utilized to supply the hydrogen burden4. Therefore, it is anticipated that this storage device will be of substantial utility in the IES. A role in energy transfer and storage can be played by IES with optimal operation5. Therefore, the economic and technical objectives of the distribution system operator (DSO) are improved by their presence in the power system5. These conditions are contingent upon the optimal energy management of IESs and their optimal planning (sitting and sizing) within the distribution system. Consequently, the technical conditions of the network can be improved by optimizing the planning and operation of renewable IESs in the distribution network using P2H and H2P technologies. This depends on the extraction of an acceptable optimization model.
Literature review
The topic of IESs in the distribution system has been the subject of numerous publications and studies, with a particular emphasis on operation and planning. A two-stage optimization method for a coupled capacity planning and operation problem, which is embedded within the economical operation of the regional IES, is presented in6. The first optimization stage of the proposed model is a regional IES planner that aims to reduce the energy and environmental costs of the system. The second stage is an operation problem that is primarily responsible for achieving the optimal operation scheme of the system. By co-optimizing the capacity configuration and power output of individual energy supply modules, the regional IES planner optimizes the installed capacity of renewable energy sources and reduces environmental costs, thereby pursuing the best interests of the region. To reduce the costs of IES operation and facilitate flexible and robust uncertainty planning, the hybrid robust-interval optimization framework was proposed in7. In order to account for the uncertainties associated with renewable energy generation output and demand response, the framework incorporated robust optimization and interval analysis. A constrained multi-objective transition algorithm was devised to solve the problem of modeling IES planning as a deterministic bi-objective optimization problem with investment operation cost and robustness as the optimization objectives. The industrial park-IES with hydrogen energy industry chain is proposed in8. Hydrogen production, transportation, and storage technologies are implemented in this system. Initially, a novel long-term hydrogen storage model that takes into account various time stages is introduced. Subsequently, hydrogen compressor models that account for various pressure ratios are implemented. A new strategy for reducing reliability costs is proposed in9in order to attain the lowest total cost. In this context, the vehicle-to-grid instrument is employed to decrease the overall system cost. The energy management model for the micro-grid in the grid-connected mode that has been presented accounts for the fluctuations in the output power of the wind turbine and photovoltaic systems, as well as the charging and discharging of plug-in electric vehicles. The modified fluid search optimization algorithm is used in this study to optimize the micro-grid operation problem. This algorithm is both innovative and effective. A grid-connected IES is proposed in10, which considers the complementarity of geothermal energy and solar energy and incorporates heat storage. A study is conducted on the multi-objective optimization problem of IES for the coupling mode of electric energy, heat energy, and cold energy. A multi-objective optimization model was developed with the objective of integrating the cost of operation, the cost of exergic efficacy, and the cost of pollution gas emission penalty by utilizing a multi-functional park as the research object.
An optimal scheduling model is proposed in11that encompasses the demand response of cooling, heating, and electricity consumption, as well as a ladder-type carbon trading mechanism. This model is based on Combined Cooling, Heat and Power system and a carbon capture device. Initially, a multi-energy and multi-type demand response model is developed, which is founded on the time-of-use electricity price and incentive mechanism. User satisfaction is employed to assess the model. Next, a carbon trading model for the integrated energy system is developed by taking into account the system’s actual carbon emissions and the ladder-type carbon trading mechanism. Ultimately, an optimal scheduling model that takes into account both low-carbon and economy is constructed by combining the operation constraints of multi-energy flow of integrated energy system with the objective function of the minimum sum of energy purchase cost, maintenance cost, carbon emission cost, and compensation cost. This transforms the problem into a mixed integer linear problem. Ref12. innovatively suggests an integrated energy system operation method that effectively reduces total operating costs and carbon emissions by enabling electric and heating loads to collaborate in demand response. Initially, the synergistic mechanism of electric and heating loads is examined, and a demand response strategy for electric and heating loads is suggested. Secondly, the electric load and thermal load demand response models are constructed based on the sensitivity of the electric load to the same electricity price and the flexibility of the thermal load, respectively. In13, a Stackelberg game theory-based operation strategy for a community IES is proposed, which considers the characteristics of supply and demand. The energy management of a smart distribution network, which includes an integrated energy system of hydrogen storage and renewable sources, is detailed in Ref14.. The objective is to evaluate the distribution system operator’s economic, operational, flexibility, and reliability objectives. The objective function is designed to reduce the costs of operation, reliability, energy losses, and network flexibility. The alternating current (AC) optimal power flow equations, network reliability limitations, and integrated energy system model all constrain the scheme. A cooperative operation method for multi-IESs is proposed in15to address the challenges encountered by an IES during independent operation, such as high operating costs and significant uncertainties in electricity prices and source-load. This method is based on a three-level Nash three-stage robust optimization. The rural comprehensive energy park distribution robust scheduling model for water-containing product breeding conservatories is proposed in16. Initially, a greenhouse model for aquaculture is developed using the principle of thermal diffusion. Subsequently, a rural integrated energy system model is developed by taking into account energy production, consumption, and storage. Reference17builds the flexible regulation models of thermal and electrical loads and introduces them to the structure expansion planning of IES. A two-stage stochastic probability optimization method integrating the uncertain operation of introducing flexible loads is then proposed to balance the additional costs of device integration and the benefits of performance promotion. Ref18. presents the unavailable operating region problem of the traditional IES and its flexibility improvement mechanism of integrating with the gas boiler, electric boiler, power-to-gas, electrical energy storage and thermal energy storage. Table 1 contains a summary of the pertinent research.
Research gaps
The following is a summary of the study openings in the field of IESs operation and planning in the power system, as indicated in Table 1:
-
The optimal operation of IESs in the distribution system is the sole factor considered in the majority of studies, such as9,10,11,12,13,14,15,1618. Nevertheless, the optimal placement and sizing of IESs can have a positive effect on the power system in addition to the operation of IESs, in order to enhance the economic and technical indices. However, the planning of IESs has been examined in conjunction with their operation in a limited number of references, including6,7,817. However, these works only examine the sizing model and do not take into account the placement model of IES.
-
Electrical energy management in IES has been the sole focus of the majority of research. However, at consumption locations, a variety of energies, including electricity, heat, and gas, are consumed. For instance, it is anticipated that a substantial number of electric vehicles powered by fuel cells will be implemented in the future in order to mitigate environmental concerns and advance technologies. Hydrogen is required for these vehicles. Consequently, it is anticipated that hydrogen consumption at consumption points will require management in addition to electric energy management. However, there is a dearth of research in the field of IESs, as evidenced by9.
-
The majority of research in the field of operation and planning of IESs has not taken into account the presence of P2H and H2P technologies. P2H is employed to generate hydrogen through the utilization of renewable energy sources. In other terms, P2H can be used as an electrolyzer (EL) to convert renewable electrical energy into hydrogen on the way to a renewable source. Hydrogen is utilized to generate electrical energy, which is denoted as H2P. It is analogous to a fuel cell (FC) that receives electrical energy and generates electrical energy at its output. Hydrogen storage is the term used to describe the combination of a hydrogen tank (HT) and P2H and H2P. This storage device operates at an acceptable level of efficacy. It can be constructed in large capacities and has a lengthy useful life. However, it is important to acknowledge that the battery is utilized as a storage device in the majority of the studies. The battery’s access to big capacities is difficult and expensive, and its construction is costly, despite its high power density and efficiency. Nevertheless, hydrogen storage can be implemented to mitigate these constraints. Furthermore, hydrogen charges may be supplied by the hydrogen storage. Previous investigations have seldom addressed this matter.
-
Renewable resources have been considered in order to achieve favorable environmental conditions and reduce operational costs in the power system. Nevertheless, wind and solar renewable sources have been implemented in the majority of studies, including6,7,8,9,10,11,12,13,15,16,17,18. Additionally, the bio-waste system (BS) is a renewable energy source that converts environmental refuse into electrical energy at its output. Nevertheless, the positive impact of BS operation on a variety of technical, economic, and environmental indicators has been assessed in a limited number of references, including14 which pertain to the IES operation.
-
The planning and operation of the IES are subject to a variety of uncertainties, including the load, renewable resources, and distribution network. Most research has employed scenario-based stochastic optimization (SBSO) to address the aforementioned uncertainties. In order to achieve a dependable solution, this approach necessitates a substantial number of scenarios. This problem results in a decrease in computation time due to the increased volume of the problem. However, minimal computing time is of particular significance in the context of power system operation issues. Some works, such as7,13,15,16,17,18, employed robust optimization to model uncertainties in order to address this issue. However, the worst-case scenarios of uncertainty parameters are the only scenario considered in this optimization. Although this issue is effective in reducing computing time, the worst-case scenario results in a high planning cost for IES. Despite the possibility that the worst-case scenario may occur with a poor degree of certainty. Thus, stochastic optimization techniques that employ the lowest scenario are required to account for these instances. The discipline of IES optimization has given less consideration to this issue.
Contributions
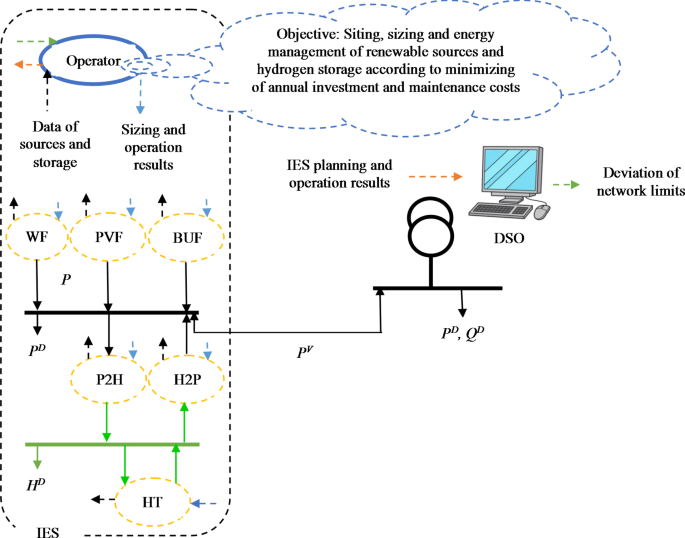
The proposed research gaps are addressed and resolved by the sitting and sizing of renewable IESs in the active distribution network (ADN) using P2H and H2P technologies, as illustrated in Fig. 1. The aforementioned IES takes into account the presence of BSs and manages electric and hydrogen energy. The optimization form is used to convey the proposed design. The total annual cost of construction and maintenance of renewable resources, P2H, H2P, and HT is minimized at the objective function. The operation and planning model of renewable resources, including wind farms (WF), photovoltaic farms (PVF), and bio-waste unit farms (BUF), as well as the operation and planning limitations of P2H, H2P, and HT, active power balance in IES, and AC optimal power flow model of ADN, are all constraints. The electrolyzer/fuel cell is included in the P2H/H2P in this article. Hydrogen is produced by the electrolyzer through the conversion of electrical energy. A portion of the hydrogen generated is utilized to fuel the hydrogen load, while the remaining portion is stored in HT. Additionally, hydrogen is supplied by HT to the fuel cell, which generates electricity at its output. The function of hydrogen storage (HS) is, of course, equivalent to the combination of H2P, P2H, and HT functions in this article. Renewable resources and the quantity of demand are uncertain in the proposed design. The final research gap is addressed by employing the stochastic optimization-based Unscented Transformation (UT) method to characterize this uncertainty and achieve a safe optimal solution. Lastly, the objectives and innovations of the present investigation are as follows:
-
The installation, sizing, and control of renewable IESs that are equipped with P2H and H2P technologies in the ADN.
-
Concurrent optimization of energy usage for both electricity and hydrogen customers in renewable IESs that are equipped with hydrogen storage.
-
Assessing the influence of the optimal performance of BSs, P2Hs, and H2Ps in IES on the technical condition of the distribution system.
-
Employing the UT approach to model uncertainty in load and renewable sources, aiming to provide a dependable solution within a short computation time.
Finally, the general contribution of this scheme is “Economic placement, sizing and energy management of renewable IES with hydrogen storage in the active distribution network according to the improvement of the operation goals of the distribution system operator based on UT approach-based stochastic optimization”.
In Sect. 2, we will discuss the planning and operation of IESs in ADN. Section 3 provides a description of the uncertainty modeling using the UT approach. Section 4 presents the quantitative results obtained from the analysis of specific instances. Ultimately, Sect. 5 concludes the paper.
Sitting and sizing of networked HS-based renewable IESs
In this article, it is assumed that the distribution network has an intelligent platform. Therefore, the term of the active distribution network was used in this article. In this network, it is expected that there is two-way coordination between the IES operator and the DSO based on Fig. 1. The IES operator is aware of the state or technical limitations of the network, therefore it determines the optimal location for itself in the network and then obtains the optimal size for resources and storage devices according to the network limitations. In the discussion of IES energy management, the IES operator is in bidirectional coordination with the renewable sources and hydrogen storage according to Fig. 1. It receives the data of these elements, and according to the network constraints announced to it by the DSO, it obtains the optimal power scheduling of the resources and storage devices and informs them. In other words, in order to implement the proposed plan on the distribution network in the real environment, it is necessary to have an intelligent platform in the network and IES.
This section presents the planning of IES, which involves the incorporation of P2H and H2P technologies in ADN. It reduces the cost of planning for IESs by considering the constraints of resources, storage devices, and the AC optimum power flow of ADN. Below is the mathematical statement of the problem:
Subject to:
-
a.
(A) Objective function: The provided equation (Eq. 1) demonstrates the minimizing of the total annual cost associated with the building and maintenance of renewable resources2and hydrogen storage19. The storage contains various components, including an EL, an HT, and a fuel cell (H2P). The cost of building and maintenance for hydrogen storage components is accounted for in Eq. (1). The cost of constructing or maintaining each element is determined by multiplying the number of elements in IES by the cost of constructing or maintaining that specific piece.
-
b.
(B) Planning-operation model of IES: The constraints of the IES planning-operation model are defined by Eqs. (2)-(14). Constraints (2)-(7) pertain to the renewable resource planning model. The active power generation received from a WF may be calculated using Eq. (2)20,21,22, which involves multiplying the number of WS, the size of each wind turbine, and the production power rate of the WF2. According to Eq. (3)23,24,25, the active power of PVF is calculated by multiplying the number, capacity, and power generation rate of PVs26. The active power generation of BUF is determined in Eq. (4) by multiplying the number, capacity, and power generation rate of the Bus2. The power rate of WF is determined by utilizing Eq. (5), which is dependent on the wind speed2. There are four operational domains for a WS. In the first region, the velocity of the wind is below the threshold speed required for energy generation, rendering the wind turbine unable to produce power. In the fourth region, the velocity of the wind exceeds the threshold speed. In order to save the mechanical components of the WS from harm, a brake mode is implemented which halts power generation. Thus, the output power of WF in the first and fourth zones is 02. In the second region, the velocity of the wind exceeds the cut-in speed but remains below the nominal speed. The power output in this region varies linearly from 0 to 1 as the wind speed increases. Within the third region, the velocity of the wind falls within the range of the designated speed and the maximum allowable speed. To avoid causing harm to the WS, the production power rate in this region is maintained at a constant value of 12. The PV power generation rate at any given point of operation, as determined by Eq. (6), is equal to the ratio of the quantity of irradiance to the amount of peak irradiance26. The power generation rate of BU per hour, as determined by Eq. (7), is equal to the ratio of BU gas to its peak value2. The operational framework of the HS, taking into account the hydrogen loads, is outlined in restrictions (8)-(12).
Constraint (8) formulates the restriction on the capacity of P2Hs14. As stated in constraint (8), the total active power consumption of P2Hs can be calculated by multiplying the number of P2Hs by the capacity of each individual P2H. Constraint (9) specifies the maximum amount of active power that H2Ps can generate14. According to constraint (9), the maximum active power generated by H2Ps is equal to the product of the number of H2Ps and the capacity of one H2P27,28,29. It is not advisable to have both the P2H and H2P systems operating simultaneously in high school. The problem is represented by constraint (10)3. Therefore, when P2Hs use active power, H2Ps are inactive and do not produce power. The converse is also accurate. The energy stored in the HT is determined using Eq. (11)14. According to this relationship30, the amount of energy stored in HT is equal to the total amount of energy stored in the previous hour, minus the energy retrieved from P2H, and minus the total amount of energy released by H2P and the hydrogen load. At hour 1:00, the amount of energy conserved from the previous hour is equal to the initial energy of HT. Thus, the parameter z is equal to one only at 1:00 h, and at all other hours it is zero. This section assumes that a portion of the hydrogen generated by P2Hs is stored in HT, while another portion is utilized to supply hydrogen loads. Thus, in Eq. (11), the inclusion of the hydrogen load will be taken into account while calculating the stored energy of HT. As stated in constraint (11), the total initial energy in HTs can be calculated by multiplying the number of HTs by the starting energy of one HT. The maximum amount of stored energy in a HT system is directly proportional to the constraint (12). As stated in constraint (12), the minimum (maximum) energy of HTs is equal to the product of the number of HTs and the minimum (maximum) energy of one HT. Ultimately, the active power equilibrium in IES aligns with constraint (13). The active power of IES is determined by the combined active power generated by renewable resources and H2Ps, subtracting the total active power consumed by P2Hs and the passive electrical load. Constraint (14) accounts for the maximum number of elements that can be inserted in IES.
-
c.
ADN operation model: The operational model of the ADN with IESs is described in constraints (15)-(23). Constraints (15)-(20) correspond to the formulation of AC power flow as described in14,31. Within these limitations, the equilibrium between the active and reactive power in the buses can be described by constraints (15) and (16) correspondingly32,33,,34. The calculation of the active and reactive power flowing via the distribution lines is determined using constraints (17) and (18)14. The voltage amplitude and angle values in the slack bus match to constraints (19) and (20), respectively35,36,37. The constraints of ADN operation are specified in constraints (21)-(23)19. Constraint (21) shows the maximum amplitude of the bus voltage limit. Constraints (22) and (23) represent the maximum apparent power that the substation and distribution line can handle, respectively31. In this section, the ADN is connected to the upstream network through the distribution substation, which is located at the slack bus (Bus 1). For Bus 1, the values of PDS and QDS are non-zero, but for other buses, they are zero.
Uncertainties model
In the proposed approach, the uncertainty parameters include wind speed (vWS), irradiance on the PV surface (IPV), generated gas by the BS (GBS), active load (PC), reactive load (QC), and hydrogen load (HC), which are represented by numbers 1 to 23. The problem at hand is a model that combines planning and operations. The power system operation involves a brief execution step, which necessitates simplifying the problem and reducing the computational burden38. In order to accomplish this objective, it is necessary to reduce the magnitude of the problem. In order to accurately represent uncertainties, the stochastic optimization method based on UT38 has been utilized in this study. The approach that has the fewest number of situations is capable of deriving a reliable and optimal solution. For each uncertainty parameter b, a total of 2b + 1 scenarios are required. In the proposed method, the value of b is set to 6, resulting in a total of 13 scenarios.
The problem is represented by the equation y = f(x). Here, y belongs to the set of real numbers raised to the power of r, and it represents an output vector with r elements. On the other hand, x belongs to the set of real numbers raised to the power of n, and it represents a vector of uncertain inputs. Furthermore, µx and σx represent the average and variability of x, respectively. The variance and covariance of uncertain quantities are calculated using both symmetric and asymmetric elements of σx. In addition, the UT technique is utilized to calculate the average (mean) and variability (covariance) of the outputs, denoted as µy and σyrespectively38. Here is a concise summary of the problem formulation process:
-
Step 1: Take 2b + 1 samples (xs) from the input data:
here, W0 shows the weight of µx (mean).
-
Step 2: Evaluate the weighting factor of individual sample points:
-
Step 3: Take 2b + 1 samples from the nonlinear function to achieve output samples using Eq. (31).
-
Step 4: Evaluate σy and µy of the output variable θ.
The proposed scheme is based on the mathematical model3940. This model contains an optimization formulation41,42,43,44. Optimization model includes objective function4546. This function minimizes or maximizes the specific term47,48,49. Optimization model includes the different constraints50,51,52,53. Constraints are in equality and inequality form54,55,56,57. To apply the optimization model on the distribution network, it is needed to smart devices58,59. These devices are based on smart algorithms and Telecommunications equipment60,61,62.
Numerical results and discussion
Case study
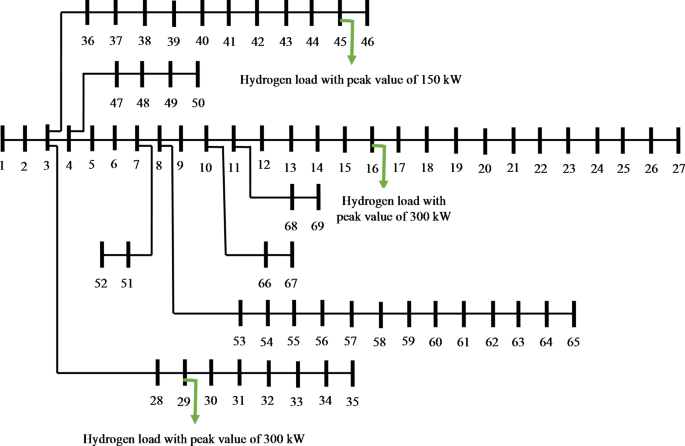
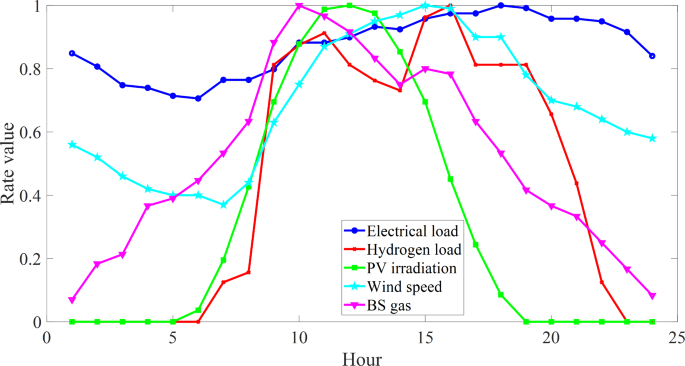
The method is implemented on the 69-bus ADN63, as depicted in Fig. 2. The network has a base power of 1 MVA, and its base voltage is 12.66 kV. Bus 1 is designated as the slack bus, with a voltage amplitude of 1 per-unit (p.u.) and a voltage angle of zero. The permissible range for the voltage amplitude is between 0.9 and 1.1 (p.u.)64,65,66,67,68. Reference63 presents the specifications of distribution lines and substations, together with the peak load data of this network. The hourly load is calculated by multiplying the peak load by the load factor69,70,71,72,73,75. Figure 314 displays the projected daily pattern of the load factor. It is anticipated that there are five buses that need to be supplied with hydrogen, and this supply should come from IESs. Figure 2 displays the precise location of the hydrogen load as well as its maximum load. The figure labeled as Fig. 375 displays the daily load factor curve for hydrogen load. Table 2 displays the specifications of renewable sources, P2H, H2P, and HT. Figure 32,26 illustrates the anticipated daily patterns of wind speed, irradiance, and BU gas relative values. In Sect. 2, a comprehensive formulation for planning of the renewable IESs equipped with hydrogen storage was stated. This model has no restrictions for implementation in different regions.
IEEE 69-bus ADN63 considering the location of hydrogen load.
Results
The proposed technique, outlined by the formulae (1)-(23), which corresponds to the UT method as discussed in Sect. 3, was implemented in a GAMS optimization software environment76. The BONMIN solver76was utilized to solve the problems in the specified program. The standard deviation of uncertainty parameters is 10%78,78,79,80,81,82. It should be noted that the simulation was done in GAMS software. In this software, the formulation of Sect. 2 is written in the GAMS software environment. At first, in this software, the amount of parameters of the problem is determined. The parameters were introduced in the Nomenclature section and their amount is stated in Sect. 4.1. Then a solver (BONMIN) is selected to solve the problem in the mentioned software. Then the software provides the amount of variables in its output. The variables were introduced in the Nomenclature section.
-
(A)
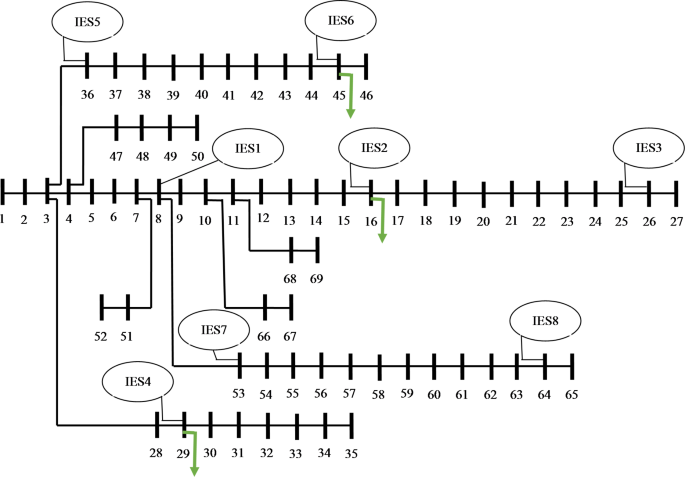
Economic planning of renewable IESs based on P2H and H2P technologies: Fig. 4 displays the optimal placement of renewable IESs with P2H and H2P technologies in the 69-bus distribution network. A maximum of eight IESs are constructed in the network described to create the most favorable conditions for achieving the operational objectives of DSO. Based on the information provided in Fig. 2, the majority of the IESs are located in the initial and intermediate buses of the feeder, while a small number of them are positioned in the buses at the termination of the feeder. The reason for this is that the distribution lines located at the start and midway of the feeder often possess a significant capacity. Consequently, it is possible to get a greater magnitude for IES. This has the potential to enhance the operational conditions of the network. The IESs positioned near the termination point of the feeder are utilized to enhance the operational conditions of the network, specifically the voltage profile. In addition, IESs are placed in the buses that carry hydrogen load, as shown in Fig. 4. This paper assumes that hydrogen loads are supplied by IESs. The appropriate size or number of renewable sources and hydrogen storage elements are presented in Table 3. Table 2 indicates that in the majority of chosen locations for IESs, the maximum number of WSs placed was five. This decision was made due to the fact that WSs have a cheaper installation cost compared to BSs and PV. Installing BSs is given secondary priority due to their cheaper installation cost compared to PV systems. However, in locations where a significant amount of renewable resources is not needed, the installation priority is given to PV systems following WS. For instance, in IES3, four WSs are required. If a different WS or BS is used in this IES, network limitations will not be accurately estimated. Therefore, PVs are placed in this IES. Table 2 indicates that the capacity of a PV system is significantly lower compared to WS and BS. Furthermore, the IESs located at the terminus of the feeder have a limited number of renewable sources due to the low capacity of the distribution lines connected to these vehicles. Nevertheless, the IESs situated in the initial and intermediate sections of the feeder possess a greater abundance of renewable resources. The quantity of hydrogen storage units is governed by the scale of renewable sources and the volume of hydrogen demand. In IESs with a substantial amount of renewable resources but without a hydrogen load, there is a significant presence of P2H systems, H2P systems, and HT. In IESs that utilize hydrogen, the quantity of P2H units exceeds that of H2P units and HT units. Consequently, a large number of energy sources are required in these IESs to ensure that the environmental and operational objectives of the DSO are achieved.
Table 4 provides the specified annual installation and maintenance cost (AIMC) for IESs and their components. Based on the data presented in the table, IESs 1, 2, 4, and 5 have the highest AIMC. This is because these IESs have the highest number of resources, including P2Hs, H2Ps, and HTs, as indicated in Table 3. IESs 3 and 8 have the lowest AIMC. These IESs have a minimal number of sources and hydrogen storage due to their positioning in the buses at the end of the feeder, as indicated by Fig. 4. The final row of Table 4 provides the AIMC for various parts of all IESs. The biggest reported expenses are associated with BUFs and energy storage devices due to their substantial quantity, as seen in the final row of Table 3. Additionally, Table 2 reveals that these devices entail significant costs for both installation and maintenance. The stated cost for hydrogen storage include the expenses associated with P2Hs, H2Ps, and HTs. Due to its lower installed capacity compared to other elements, PVFs have the lowest AIMC. In order to install eight IESs that match the parameters specified in Table 3, a total planned cost of 1,462,950 M$ per year is required.
Table 3 Optimal capacity of sources and storages in IESs. Table 4 AIMC of IESs. -
(B)
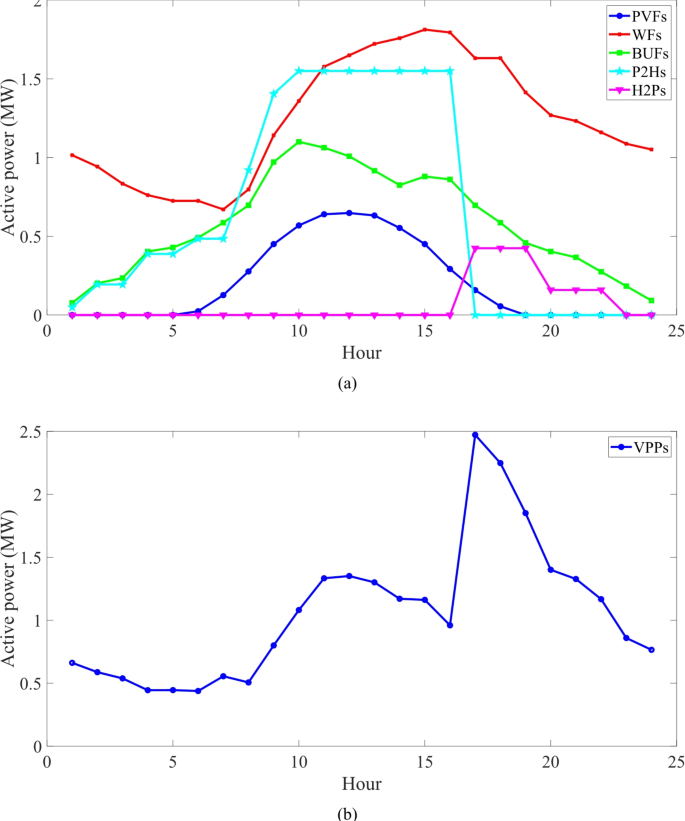
Investigating the performance of renewable IESs: Fig. 5 illustrates the projected daily pattern of the active power of IESs and their components, using the ideal quantity specified in Table 3. By referring to Fig. 5a and comparing it with Fig. 3, we observe that the temporal changes in the production power of renewable resources align with the temporal fluctuations in the rate of natural processes. For instance, the daily power curve of wind farms closely resembles the curve of wind speed, differing only in numerical values. Table 3 indicates that a total of 37 WSs have been installed in all IESs. According to Table 2, the power capacity of each WS is around 50 kW. According to Fig. 5a, WFs have the capability to inject a maximum active power of around 1.85 MW into IESs. PVFs and BUFs provide a maximum active power injection of 0.65 MW and 1.1 MW, respectively, to all IESs. The graph in Fig. 5a illustrates the daily active power curve of P2Hs and H2Ps. Table 3 indicates that there are 19 HT installations with a capacity of 200 kWh in IESs. The minimum energy stored in them is equivalent to 20 kWh. Hence, HT systems have the capacity to obtain and store energy equivalent to 3420 kWh or 3.42 MWh from IESs. Based on Fig. 2, the maximum amount of hydrogen consumed is 750 kW. Hence, the quantity of hydrogen energy utilized by these loads, as indicated by the load factor curve in Fig. 3, is approximately 8.1 MWh. Hence, the output of P2Hs should generate a total energy of 11.52 MWh, which is the sum of 3.42 MWh and 8.1 MWh. Given that the efficiency of the system in Table 2 is 75%, they should expect to get around 15.36 MWh of energy from IESs. H2Ps can solely convert the stored energy in HTs into electrical energy for IESs. Based on the data in Table 2, the efficiency of H2Ps is 51%. Consequently, H2Ps generate 1.75 MWh (0.51 × 3.42) of electrical energy as their output. According to Fig. 5a, the active power level of P2Hs is significantly greater than that of H2Ps. This is also evident in Table 3. The installed capacity of P2H is significantly greater than H2P. P2Hs are operational during non-peak and mid-peak timeframes, specifically from 1:00 to 16:00. According to Fig. 5a, renewable sources generate a significant amount of power during the off-peak hours of 1:00–16:00. To prevent excessive voltage in the distribution network during these hours, P2H systems get electricity from renewable sources at this time. However, between the hours of 17:00 and 22:00, when network usage is at its highest, P2Hs are deactivated and H2Ps are utilized to supply active power to IESs or the distribution network. This helps to mitigate the significant voltage drop that occurs during peak hours. Figure 5b displays the daily active power curve of IESs. The power can be located in Eq. (13). According to Fig. 5b, the IESs generate electrical energy continuously. Their highest level of power generation is throughout the mid-load and peak hours, specifically from 8:00 to 22:00. According to Fig. 5a, renewable sources and H2Ps generate a substantial amount of active power during these specific hours.
-
(C)
Evaluating the operation status of the ADN: For the purpose of evaluating the proposed plan to improve the operational conditions of the distribution system, the following study components are taken into account:
-
Case I: Load flow analysis of the network.
-
Case II: Suggested design by taking only renewable sources model into account in IES.
-
Case III: Case II + HSs without hydrogen load.
-
Case IV: Case II + HSs with hydrogen load.
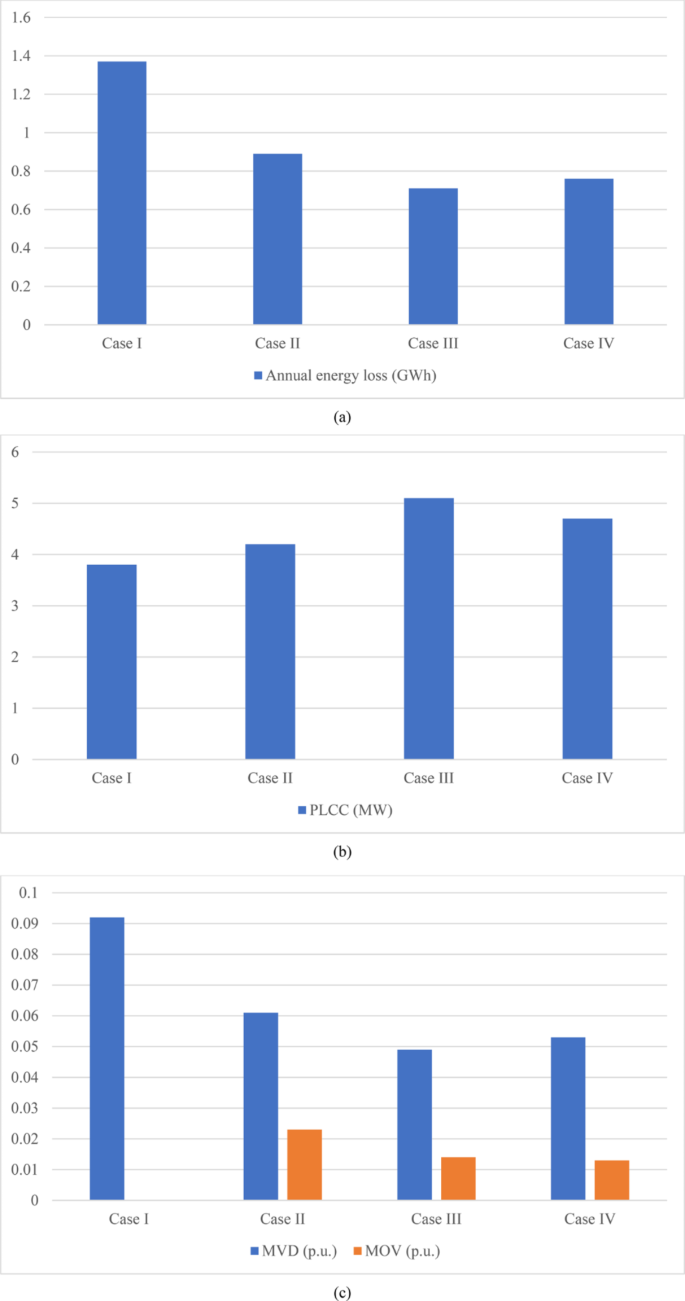
Figure 6 presents operational metrics for several scenarios, including annual energy loss, maximum voltage drop (MVD), maximum overvoltage (MOV), and peak load carrying capability (PLCC). PLCC refers to the ability of ADN to supply the maximum power demand using the daily coefficient curve, as shown in Fig. 3. The most unfavorable state of the indicated indices has been observed in instance I. Therefore, it exhibits the most significant energy losses and MVD. This case also examines the minimum PLCC. In IESs corresponding to case II, where only renewable resources are present, the energy loss and MVD are reduced by approximately 35% and 33.7% compared to case I. Additionally, PLCC exhibits an enhancement of around 10.5% when compared to power flow analyses. The specified requirements are necessary in order to generate a magnitude of 0.023 p.u. in the ADN. In case III, the inclusion of hydrogen storage and renewable sources is taken into account in the IES. In case III, the operating indices, such as energy loss and MVD, are reduced by approximately 48.2% and 46.7%, respectively, compared to case I. The MOV is decreased by approximately 39.1% compared to case II, but the PLCC is increased by approximately 34.2% compared to case I. In the fourth case, the inclusion of a hydrogen load in the IES is considered. When compared to case III, this results in a higher amount of energy loss and MVD, and also causes a decrease in PLCC. Nevertheless, case IV has successfully decreased the energy loss and MVD by approximately 44.5% and 42.4% respectively compared to case I. PLCC has a 23.7% improvement compared to case I. In case IV, the magnitude of the MOV is decreased by 43.5% compared to case II.
-
-
(D)
The state of convergence of the suggested design: Table 5presents the values of the objective function (AIMC) for various mathematical solvers, namely BONMIN, BARON, DICOPT, KNITRO, and OQNLP76, in the uncertainty model using the UT method and scenario-based stochastic optimization (SBSO)83. The solvers listed have a toolbox in the GAMS program and are specifically designed to address mixed-integer nonlinear problems. Within the context of SBSO, the roulette wheel mechanism initially produces a large number of potential possibilities for the unclear parameters of the problem. The magnitude of each uncertainty in each scenario is determined based on its average value and standard deviation. Next, the normal probability function is employed to compute the probability of each uncertain parameter. The likelihood of each generated scenario is determined by multiplying the probabilities of the uncertainty. The Kantorovich technique chooses a predetermined quantity of created scenarios and applies them to the situation at hand. This approach chooses the scenarios with the shortest distance between them. Comprehensive information about SBSO can be found in reference83. Table 5 reveals that the BONMIN method possesses an objective function value of $1,462,950, whilst the other algorithms have AIMC quantities exceeding $1,465,000. Furthermore, the computational time required by BONMIN is 41.2 min, which surpasses the 58-minute mark for other solvers. Thus, BONMIN has successfully achieved the most optimal solution in the least amount of processing time when compared to other mathematical algorithms for the suggested design. Furthermore, in the case of a low scenario number in SBSO, there is a significant disparity between the AIMC result and the UT technique. However, the discrepancy in calculations between the numerous situations, exceeding 100 in number, is minimal. Put simply, the SBSO approach has achieved a dependable solution in a greater range of situations, but the UT method is capable of extracting a reliable solution with significantly fewer scenarios. As a result, UT has a significantly shorter computing time compared to SBSO.
Table 5 AIMC of IESs and calculation time of the proposed scheme based on the different solvers in the UT method and SBSO.
Conclusion
This study presents the placement and sizing of a renewable IES that includes P2H and H2P technologies. The goal is to determine the ideal operating parameters for this system in the ADN. An integrated energy system is implemented to handle electrical and hydrogen energy. P2H and H2P, in conjunction with the HT, collectively constitute a hydrogen storage system. An optimization model was employed for the proposed scheme. The problem at hand involves the planning of integrated energy systems, with the goal of minimizing the total annual cost of constructing and maintaining resources and hydrogen storages. This is done by considering the limitations of the planning and operation model for these elements, as well as the AC optimal power flow model of the network. The UT approach was used to accurately describe uncertainty related to load and renewable phenomena. Based on the numerical results, it is common to install IES in the first and middle buses of the feeder. These interconnected systems can possess a substantial magnitude. Nevertheless, a limited quantity of these units is positioned at the conclusion of the feeder to optimize the operational condition of the system. The dimensions of the resources, P2Hs, H2Ps, and HTs in these units are small. Consequently, the integrated energy systems positioned at the end of the feeders have the lowest planning cost. The largest planning cost is attained in the integrated energy systems positioned at the beginning of the feeder and with hydrogen load. P2H exhibits significantly more capacity than H2P in terms of supplying the hydrogen need and storing the energy in the HT. By achieving maximum efficiency in resource use and hydrogen storage, integrated energy systems within the distribution network function as energy generators. Hence, the technique improves the operational conditions by 23-45% in comparison to power flow analysis. In other words, in this condition, energy loss and voltage drop have decreased by 44.5% and 42.4%, respectively, and peak load carrying capability has increased by 23.7%. Compared to the network with renewable resources, the integrated energy system equipped with hydrogen storage has been able to reduce overvoltage by about 43.5%. The BONMIN method discovered a more optimal solution for the proposed design with minimal computational time in comparison to alternative mathematical solvers. The UT approach, compared to SBSO, can efficiently produce a trustworthy solution with minimal computational time. Finally, the obtained numerical results show the advantages and innovations of this project as follows:
-
Optimal placement and sizing of the renewable integrated energy system with P2H and H2P technologies in the active distribution network has been able to improve the status of operational indicators such as energy losses, voltage profile and peak load carrying capability compared to load flow studies.
-
The energy management of the hydrogen storage in the renewable integrated energy system has been able to act as an energy storage, feed the hydrogen load, reduce the planning cost, and it has caused integrated energy system to appear as an energy producer.
-
The presence of renewable resources such as wind, solar and bio-waste systems in the integrated energy system has been able to improve the state of network operation compared to load flow studies.
-
The UT method has been able to provide a reliable optimal solution for the proposed design with a low number of scenarios, while SBSO has a reliable solution with a high number of scenarios. Therefore, the UT method has the lowest calculation time.
Data availability
All data generated or analyzed during this study are included in this published article, Sect. 4.1. Also, the datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Abbreviations
- AIMC:
-
Annual investment and maintenance cost ($/year)
- EHT
: -
Energy storage in the hydrogen tank (HT) in MWh
- Ne
: -
Number of a specific element in integrated energy system (IES). e refers to wind system (WS), photovoltaic (PV), bio-waste system (BS), P2H, H2P, and HT
(bar{N}^{e})
:-
Maximum number of a specific element in IES. e is WS, PV, BS, P2H, H2P, and HT
- NWS, NPV, NBS, NP2H, NH2P, NHT
: -
The number of installed WS, PV, BS, P2H, H2P, and HT in the IES
(begin{gathered} bar{N}^{{WS}} ,bar{N}^{{PV}} ,bar{N}^{{BS}} ,bar{N}^{{P2H}} hfill bar{N}^{{H2P}} ,bar{N}^{{HT}} hfill end{gathered})
:-
Maximum number of WS, PV, BS, P2H, H2P, and HT in the IES
- PDL, PDS
: -
Active power of the line and distribution substation, and load not-supplied (MW)
- PWF, PPVF, PBUF, PP2H, PH2P, PV
: -
Active power of wind farm (WF), PV farm (PVF), bio-waste unit farm (BUF), P2H, H2P, and IES (MW)
- QDL, QDS
: -
Reactive power of the line and distribution substation (MVAr)
- V,α:
-
Amplitude (p.u.) and voltage angle (rad)
- ICP2H, ICH2P, ICHT
: -
Annual construction cost of P2H, H2P, and HT ($/year)
- ICWS, ICPV, ICBS
: -
Annual construction cost of WS, PV, and BS ($/year)
- MCP2H, MCH2P, MCHT
: -
Annual repair and maintenance cost of P2H, H2P, and HT ($/year)
- MCWS, MCPV, MCBS
: -
Annual repair and maintenance cost of WS, PV, and BS ($/year)
- BDL, GDL
: -
Susceptance and conductivity of the distribution line (p.u.)
- CDL
: -
Incidence matrix of buses and distribution lines
(hat{E}^{{HT}} ,underset{raise0.3emhbox{$smash{scriptscriptstyle-}$}}{E} ^{{HT}} ,bar{E}^{{HT}})
:-
Initial energy, minimum and maximum energy stored in HT (MWh)
(bar{I}^{{PV}} ,bar{G}^{{BS}})
:-
The maximum amount of irradiance (kW/m2) and gas generation by BS (m3)
- PD, QD, HD
: -
Active power (MW) and reactive power (MVAr) of electric consumer, hydrogen load (MW)
(begin{gathered} bar{P}^{{WS}} ,bar{P}^{{PV}} ,bar{P}^{{BS}} ,bar{P}^{{P2H}} hfill bar{P}^{{H2P}} end{gathered})
:-
Maximum active power (capacity) of WS, PV, BS, P2H, and H2P (MW)
(begin{gathered} bar{S}^{{DS}} ,bar{S}^{{DL}} end{gathered})
:-
Maximum apparent power (capacity) of substation and distribution line (MVA)
(underset{raise0.3emhbox{$smash{scriptscriptstyle-}$}}{V} ,bar{V})
:-
The minimum and maximum voltage amplitude (p.u.)
- vC−IN, vC−OUT, vR
: -
Cut-in, cut-out, and rated wind speed (m/s)
- vWS, IPV, GBS
: -
Wind speed (m/s), irradiance (kW/m2), and BS gas production (m3)
- ηP2H, ηH2P
: -
Efficiency of P2H and H2P
- ρ:
-
The probability of the scenario
- φWS, φPV, φBS
: -
Power generation rate for WS, PV, and BS
- j:
-
Index of bus
- n, h, s:
-
Index of bus, operation time, scenario
References
-
Wu, J. et al. Integrated energy systems. Appl. Energy 167, 155–157 (2016).
-
Khalafian, F. et al. Capabilities of compressed air energy storage in the economic design of renewable off-grid system to supply electricity and heat costumers and smart charging-based electric vehicles. J. Energy Storage 78, 109888 (2024).
-
Wang, W., Yuan, B., Sun, Q. & Wennersten, R. Application of energy storage in integrated energy systems—A solution to fluctuation and uncertainty of renewable energy. J. Energy Storage 52, 104812 (2022).
-
Usman, M. R. Hydrogen storage methods: Review and current status. Renew. Sustain. Energy Rev. 167, 112743 (2022).
-
Huang, Z., Fang, B. & Deng, J. Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system. Protect. Control Modern Power Syst. 5, 1–8 (2020).
-
Wang, Y. et al. Planning and operation method of the regional integrated energy system considering economy and environment. Energy 171, 731–750 (2019).
-
Dong, Y., Zhang, H., Ma, P., Wang, C. & Zhou, X. A hybrid robust-interval optimization approach for integrated energy systems planning under uncertainties. Energy 274, 127267 (2023).
-
Lin, J. & Cai, R. Optimal planning for industrial park-integrated energy system with hydrogen energy industry chain. Int. J. Hydrogen Energy 48(50), 19046–19059 (2023).
-
Hai, T. & Zhou, J. Optimal planning and design of integrated energy systems in a microgrid incorporating electric vehicles and fuel cell system. J. Power Sources 561, 232694 (2023).
-
Wu, X., Liao, B., Su, Y. & Li, S. Multi-objective and multi-algorithm operation optimization of integrated energy system considering ground source energy and solar energy. Int. J. Electrical Power Energy Syst. 144, 108529 (2023).
-
Yang, P., Jiang, H., Liu, C., Kang, L. & Wang, C. Coordinated optimization scheduling operation of integrated energy system considering demand response and carbon trading mechanism. Int. J. Electrical Energy Syst. 147, 108902 (2023).
-
Wang, Y., Li, Y., Zhang, Y., Xu, M. & Li, D. Optimized operation of integrated energy systems accounting for synergistic electricity and heat demand response under heat load flexibility. Appl. Thermal Eng. 243, 122640 (2024).
-
Shi, S., Gao, Q., Ji, Y., Liu, J., & Chen, H. (2024). Operation strategy for community integrated energy system considering source-load characteristics based on Stackelberg game. Appl. Thermal Eng., 254, 123739.
-
Liang, H. & Pirouzi, S. Energy management system based on economic Flexi-reliable operation for the smart distribution network including integrated energy system of hydrogen storage and renewable sources. Energy 293, 130745 (2024).
-
Zhang, Z. & Fedorovich, K. S. Optimal operation of multi-integrated energy system based on multi-level Nash multi-stage robust. Appl. Energy 358, 122557 (2024).
-
Wang, Q., Xiao, Y., Tan, H. & Mohamed, M. A. Day-Ahead scheduling of rural integrated energy systems based on distributionally robust optimization theory. Applied Thermal Engineering 246, 123001 (2024).
-
Wu, M., Yan, R., Zhang, J., Fan, J., Wang, J., Bai, Z., … & Hu, K. (2024). An enhanced stochastic optimization for more flexibility on integrated energy system with flexible loads and a high penetration level of renewables. Renewable Energy, 227, 120502.
-
Yan, R., Wang, J., Huo, S., Qin, Y., Zhang, J., Tang, S., … & Zhou, L. (2023). Flexibility improvement and stochastic multi-scenario hybrid optimization for an integrated energy system with high-proportion renewable energy. Energy, 263, 125779.
-
Sun, H. et al. Designing framework of hybrid photovoltaic-biowaste energy system with hydrogen storage considering economic and technical indices using whale optimization algorithm. Energy 238, 121555 (2022).
-
Leng, Hua, et al. A new wind power prediction method based on ridgelet transforms, hybrid feature selection and closed-loop forecasting. Adv. Eng. Inf. 36, 20–30 (2018).
-
Mir, Mahdi, et al. Application of hybrid forecast engine based intelligent algorithm and feature selection for wind signal prediction. Evolv. Syst. 11(4), 559–573 (2020).
-
Zhu, Ligui, et al. Multi-criteria evaluation and optimization of a novel thermodynamic cycle based on a wind farm, Kalina cycle and storage system: an effort to improve efficiency and sustainability. Sustain. Cities Soc. 96, 104718 (2023).
-
Bo, Gao, et al. Optimum structure of a combined wind/photovoltaic/fuel cell-based on amended Dragon Fly optimization algorithm: a case study. Energy Sources, Part A: Rec. Utilization, Environ. Effects 44(3), 7109–7131 (2022).
-
Mehrpooya, Mehdi, et al. “Numerical investigation of a new combined energy system includes parabolic dish solar collector, Stirling engine and thermoelectric device.” International Journal of Energy Research 45.11 (2021): 16436–16455.
-
Ghadimi, Noradin, et al. “An innovative technique for optimization and sensitivity analysis of a PV/DG/BESS based on converged Henry gas solubility optimizer: A case study.” IET Generation, Transmission & Distribution 17.21 (2023): 4735–4749.
-
Maleki, A. & Askarzadeh, A. Optimal sizing of a PV/wind/diesel system with battery storage for electrification to an off-grid remote region: A case study of Rafsanjan. Iran. Sustainable Energy Technologies and Assessments 7, 147–153 (2014).
-
Han, E. & Ghadimi, N. Model identification of proton-exchange membrane fuel cells based on a hybrid convolutional neural network and extreme learning machine optimized by improved honey badger algorithm. Sustainable Energy Technologies and Assessments 52, 102005 (2022).
-
Yuan, Keke, et al. “Optimal parameters estimation of the proton exchange membrane fuel cell stacks using a combined owl search algorithm.” Energy Sources, Part A: Recovery, Utilization, and Environmental Effects 45.4 (2023): 11712–11732.
-
Guo, X. & Ghadimi, N. Optimal design of the proton-exchange membrane fuel cell connected to the network utilizing an improved version of the metaheuristic algorithm. Sustainability 15(18), 13877 (2023).
-
Liu, Jun, et al. “An IGDT-based risk-involved optimal bidding strategy for hydrogen storage-based intelligent parking lot of electric vehicles.” Journal of Energy Storage 27 (2020): 101057.
-
Pirouzi, S., Zadehbagheri, M., & Behzadpoor, S. (2024). Optimal placement of distributed generation and distributed automation in the distribution grid based on operation, reliability, and economic objective of distribution system operator. Electrical Engineering, 1–14.
-
Jiang, Wei, et al. “Optimal economic scheduling of microgrids considering renewable energy sources based on energy hub model using demand response and improved water wave optimization algorithm.” Journal of Energy Storage 55 (2022): 105311.
-
Dehghani, Moslem, et al. “Blockchain-based securing of data exchange in a power transmission system considering congestion management and social welfare.” Sustainability 13.1 (2020): 90.
-
Chen, Liang, et al. “Optimal modeling of combined cooling, heating, and power systems using developed African Vulture Optimization: a case study in watersport complex.” Energy Sources, Part A: Recovery, Utilization, and Environmental Effects 44.2 (2022): 4296–4317.
-
Yuan, Zhi, et al. “Probabilistic decomposition‐based security constrained transmission expansion planning incorporating distributed series reactor.” IET Generation, Transmission & Distribution 14.17 (2020): 3478–3487.
-
Eslami, Mahdiyeh, et al. “A new formulation to reduce the number of variables and constraints to expedite SCUC in bulky power systems.” Proceedings of the national academy of sciences, india section a: physical sciences 89 (2019): 311–321.
-
Nejad, Hadi Chahkandi, et al. “Reliability based optimal allocation of distributed generations in transmission systems under demand response program.” Electric Power Systems Research 176 (2019): 105952.
-
Aien, M., Fotuhi-Firuzabad, M. & Aminifar, F. Probabilistic load flow in correlated uncertain environment using unscented transformation. IEEE Transactions on Power systems 27(4), 2233–2241 (2012).
-
Hamian, Melika, et al. “A framework to expedite joint energy-reserve payment cost minimization using a custom-designed method based on mixed integer genetic algorithm.” Engineering Applications of Artificial Intelligence 72 (2018): 203–212.
-
Abedinia, Oveis, et al. “Optimal offering and bidding strategies of renewable energy based large consumer using a novel hybrid robust-stochastic approach.” Journal of cleaner production 215 (2019): 878–889.
-
Khodaei, Hossein, et al. “Fuzzy-based heat and power hub models for cost-emission operation of an industrial consumer using compromise programming.” Applied Thermal Engineering 137 (2018): 395–405.
-
Mohammadi, Mohsen, et al. “Small-scale building load forecast based on hybrid forecast engine.” Neural Processing Letters 48 (2018): 329–351.
-
Cao, Yan, et al. “Optimal operation of CCHP and renewable generation-based energy hub considering environmental perspective: An epsilon constraint and fuzzy methods.” Sustainable Energy, Grids and Networks 20 (2019): 100274.
-
Akbary, Paria, et al. “Extracting appropriate nodal marginal prices for all types of committed reserve.” Computational Economics 53 (2019): 1–26.
-
Yu, D. & Ghadimi, N. Reliability constraint stochastic UC by considering the correlation of random variables with Copula theory. IET Renewable power generation 13(14), 2587–2593 (2019).
-
Saeedi, Mohammadhossein, et al. “Robust optimization based optimal chiller loading under cooling demand uncertainty.” Applied Thermal Engineering 148 (2019): 1081–1091.
-
Karamnejadi Azar, Keyvan, et al. “Developed design of battle royale optimizer for the optimum identification of solid oxide fuel cell.” Sustainability 14.16 (2022): 9882.
-
Abedinia, Oveis, et al. “A new combinatory approach for wind power forecasting.” IEEE Systems Journal 14.3 (2020): 4614–4625.
-
Meng, Qing, et al. “A single-phase transformer-less grid-tied inverter based on switched capacitor for PV application.” Journal of Control, Automation and Electrical Systems 31 (2020): 257–270.
-
Mahdinia, Saeideh, et al. “Optimization of PEMFC model parameters using meta-heuristics.” Sustainability 13.22 (2021): 12771.
-
Rezaie, Mehrdad, et al. “Model parameters estimation of the proton exchange membrane fuel cell by a Modified Golden Jackal Optimization.” Sustainable Energy Technologies and Assessments 53 (2022): 102657.
-
Guo, Haibing, et al. “Parameter extraction of the SOFC mathematical model based on fractional order version of dragonfly algorithm.” International Journal of Hydrogen Energy 47.57 (2022): 24059–24068.
-
Ye, Haixiong, et al. “High step-up interleaved dc/dc converter with high efficiency.” Energy sources, Part A: recovery, utilization, and environmental effects (2020): 1–20.
-
Duan, Fude, et al. “Model parameters identification of the PEMFCs using an improved design of Crow Search Algorithm.” International Journal of Hydrogen Energy 47.79 (2022): 33839–33849.
-
Zhang, J., Khayatnezhad, M. & Ghadimi, N. Optimal model evaluation of the proton-exchange membrane fuel cells based on deep learning and modified African Vulture Optimization Algorithm. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects 44(1), 287–305 (2022).
-
Chang, Le., Zhixin, Wu. & Ghadimi, N. A new biomass-based hybrid energy system integrated with a flue gas condensation process and energy storage option: an effort to mitigate environmental hazards. Process Safety and Environmental Protection 177, 959–975 (2023).
-
Li, Shunlei, et al. “Evaluating the efficiency of CCHP systems in Xinjiang Uygur Autonomous Region: an optimal strategy based on improved mother optimization algorithm.” Case Studies in Thermal Engineering 54 (2024): 104005.
-
Ghiasi, Mohammad, et al. “A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: Past, present and future.” Electric Power Systems Research 215 (2023): 108975.
-
Gong, Z., Li, Lu. & Ghadimi, N. SOFC stack modeling: a hybrid RBF-ANN and flexible Al-Biruni Earth radius optimization approach. International Journal of Low-Carbon Technologies 19, 1337–1350 (2024).
-
Han, Mengdi, et al. “Timely detection of skin cancer: An AI-based approach on the basis of the integration of Echo State Network and adapted Seasons Optimization Algorithm.” Biomedical Signal Processing and Control 94 (2024): 106324.
-
Liu, H. & Ghadimi, N. Hybrid convolutional neural network and Flexible Dwarf Mongoose Optimization Algorithm for strong kidney stone diagnosis. Biomedical Signal Processing and Control 91, 106024 (2024).
-
Zhang, Li, et al. “A deep learning outline aimed at prompt skin cancer detection utilizing gated recurrent unit networks and improved orca predation algorithm.” Biomedical Signal Processing and Control 90 (2024): 105858.
-
Kadir, A. F. A., Mohamed, A., Shareef, H. & Wanik, M. Z. C. Optimal placement and sizing of distributed generations in distribution systems for minimizing losses and THD_v using evolutionary programming. Turkish Journal of Electrical Engineering and Computer Sciences 21(8), 2269–2282 (2013).
-
Navesi, R. B., Nazarpour, D., Ghanizadeh, R. & Alemi, P. Switchable capacitor bank coordination and dynamic network reconfiguration for improving operation of distribution network integrated with renewable energy resources. Journal of modern power systems and clean energy 10(3), 637–646 (2021).
-
Yan, Z., Gao, Z., Navesi, R. B., Jadidoleslam, M. & Pirouzi, A. Smart distribution network operation based on energy management system considering economic-technical goals of network operator. Energy Reports 9, 4466–4477 (2023).
-
Bayat, A., Bagheri, A. & Navesi, R. B. A real-time PMU-based optimal operation strategy for active and reactive power sources in smart distribution systems. Electric Power Systems Research 225, 109842 (2023).
-
Navesi, R. B., Jadidoleslam, M., Moradi-Shahrbabak, Z. & Naghibi, A. F. Capability of battery-based integrated renewable energy systems in the energy management and flexibility regulation of smart distribution networks considering energy and flexibility markets. Journal of Energy Storage 98, 113007 (2024).
-
Naghibi, A. F., Koochaki, A. & Gatabi, M. Optimal Protection Coordination of Directional Overcurrent Relays using Shuffled Frog Leaping in Smart Grids. Majlesi Journal of Mechatronic Systems 8(4), 25–31 (2019).
-
Akbari, E. et al. Multi-objective economic operation of smart distribution network with renewable-flexible virtual power plants considering voltage security index. Scientific Reports 14(1), 19136 (2024).
-
Zadehbagheri, M., et al. (2024). Resiliency-constrained placement and sizing of virtual power plants in the distribution network considering extreme weather events. Electrical Engineering, 1–17.
-
Oboudi, M. H., et al. (2024). Reliability-constrained transmission expansion planning based on simultaneous forecasting method of loads and renewable generations. Electrical Engineering, 1–21.
-
Zadehbagheri, M. et al. The impact of sustainable energy technologies and demand response programs on the hub’s planning by the practical consideration of tidal turbines as a novel option. Energy Reports 9, 5473–5490 (2023).
-
Norouzi, M. et al. Risk-averse and flexi-intelligent scheduling of microgrids based on hybrid Boltzmann machines and cascade neural network forecasting. Applied Energy 348, 121573 (2023).
-
Yao, M., et al. (2023). Stochastic economic operation of coupling unit of flexi-renewable virtual power plant and electric spring in the smart distribution network. IEEE Access.
-
Wang, Q., Wang, Y. & Chen, Z. Stackelberg equilibrium-based energy management strategy for regional integrated electricity–hydrogen market. Frontiers in Energy Research 11, 1169089 (2023).
-
Generalized Algebraic Modeling Systems (GAMS). [Online]. Available: http://www.gams.com.
-
Sabzalian, M. H. et al. Two-Layer Coordinated Energy Management Method in the Smart Distribution Network including Multi-Microgrid Based on the Hybrid Flexible and Securable Operation Strategy. International Transactions on Electrical Energy Systems 2022(1), 3378538 (2022).
-
Bagherzadeh, L. et al. Coordinated flexible energy and self-healing management according to the multi-agent system-based restoration scheme in active distribution network. IET Renewable Power Generation 15(8), 1765–1777 (2021).
-
Norouzi, M., et al. (2019, September). Enhancing distribution network indices using electric spring under renewable generation permission. In 2019 International Conference on Smart Energy Systems and Technologies (SEST) (pp. 1–6). IEEE.
-
Pirouzi, S., Latify, M. A., & Yousefi, G. R. (2015, May). Investigation on reactive power support capability of PEVs in distribution network operation. In 2015 23rd Iranian Conference on Electrical Engineering (pp. 1591–1596). IEEE.
-
Dini, A. et al. Security-Constrained generation and transmission expansion planning based on optimal bidding in the energy and reserve markets. Electric Power Systems Research 193, 107017 (2021).
-
Ansari, M. R. et al. Renewable generation and transmission expansion planning coordination with energy storage system: a flexibility point of view. Applied Sciences 11(8), 3303 (2021).
-
Jamali, A. et al. Self-scheduling approach to coordinating wind power producers with energy storage and demand response. IEEE Transactions on Sustainable Energy 11(3), 1210–1219 (2019).
Author information
Authors and Affiliations
Contributions
Ahad Faraji Naghibi: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data Curation, Writing – Original Draft.Ehsan Akbari: Supervisor, Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data Curation, Writing – Original Draft.Saeid Shahmoradi: Investigation, Resources, Data Curation, Writing – Original Draft.Sasan Pirouzi: Methodology, Software, Validation, Formal analysis, Data Curation, Writing – Original Draft.Amid Shahbazi: Investigation, Resources, Data Curation, Writing – Original Draft.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Naghibi, A.F., Akbari, E., Shahmoradi, S. et al. Stochastic economic sizing and placement of renewable integrated energy system with combined hydrogen and power technology in the active distribution network.
Sci Rep 14, 28354 (2024). https://doi.org/10.1038/s41598-024-79222-4
-
Received: 22 August 2024
-
Accepted: 07 November 2024
-
Published: 16 November 2024
-
DOI: https://doi.org/10.1038/s41598-024-79222-4
Keywords
Search
RECENT PRESS RELEASES
Related Post