The multidimensional relationship between renewable energy deployment and carbon dioxide emissions in high-income nations
November 20, 2024
Abstract
Cross-national research has found that the decarbonization effect of renewable energy development is relatively weak in high-income nations. It is crucial to identify effective points of intervention to enhance renewables’ decarbonization effect. Using a multidimensional analytical framework, this study examines whether certain structural components of high-income nations’ CO2 emissions are particularly susceptible to barriers to decarbonization and therefore are less effectively mitigated by renewable energy development. Analyzing a panel dataset covering 33 high-income nations from 1996 to 2019, I identify a pattern of uneven decarbonization. Renewable energy development has mitigated production-based emissions with increasing effectiveness over time; however, the mitigation effect has been largely confined to emissions from domestic-oriented supply chain activities. Meanwhile, renewables’ inability to mitigate emissions embodied in exports and direct end-user emissions has largely persisted over time. Additionally, developing renewable energy has not spurred growth in emissions in imports, indicating that it has not intensified carbon leakage.
Introduction
Collectively, nations worldwide are falling short of the targets outlined in the Paris Agreement to substantially reduce greenhouse gas emissions and avert catastrophic climate change1. The urgency for climate actions underscores the critical need to optimize the decarbonization effect of renewable energy development, a key element of pathways to climate mitigation. Prior research has examined barriers to decarbonization, such as the entrenched fossil fuel regime and the fuel market rebound effect, that hinder the effectiveness of renewable energy development in displacing fossil fuels and reducing CO2 emissions2,3,4,5,6,7. Notably, cross-national studies find that renewables’ overall decarbonization effect on nations’ CO2 emissions tends to be relatively weak in high-income nations8,9,10,11, despite that these nations generally have greater financial and technological capability for the renewable energy transition12. It is crucial to identify effective leverage points to improve renewables’ decarbonization effect in high-income nations, many of which are major CO2 emitters13.
Prior cross-national research focuses on how renewables affect nations’ production-based account (PBA) of emissions, an aggregate measure of emissions. However, CO2 is emitted by a myriad of human activities that may be unevenly affected by broad social, economic, and political forces, including those hampering the decarbonization effect of renewables. As a result, how effective renewable energy development is in curbing emissions likely differs across emission components generated by different types of human activities. The relatively weak decarbonization effect of renewables in high-income nations might be disproportionally attributed to certain emission components that are particularly susceptible to the barriers to decarbonization, yet, these emission components have not been adequately identified in the existing cross-national research.
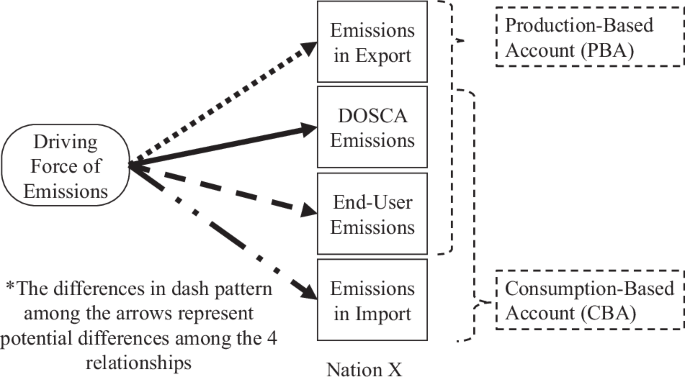
The current study fills this gap by engaging a novel analytical framework called multidimensional emissions profile (MEP), which situates nations’ emissions into 4 structural components: (1) emissions from domestic-oriented supply chain activities (DOSCA); (2) emissions embodied in exports; (3) direct emissions from end-user activities; and (4) emissions embodied in imports14. Among the first three emission components, I identify which components are more susceptible to the barriers to decarbonization and therefore less effectively mitigated by renewable energy development. I also assess how renewables’ decarbonization effect has changed over time for each emission component, which indicates whether prior strategies on deploying renewable energies have become more effective in overcoming the barriers to decarbonization. Additionally, I investigate whether developing renewable energy exacerbates carbon leakage and spurs emissions in imports. I analyze a panel dataset covering 33 high-income nations from 1996 to 2019.
First, I provide a brief review of the literature on the barriers to the decarbonization effect of renewable energy development. Developing renewable energy is an important strategy to reduce nations’ CO2 emissions15,16. However, its decarbonization effect is often found to be relatively weak in cross-national studies of high-income country groups10,11,17. This is consistent with a moderation effect observed by Thombs8 and York and McGee9, where income level suppresses the negative association between renewables and emissions: in higher-income nations, per unit increase in renewable energy consumption is associated with a smaller reduction in CO2 emissions compared to in lower-income nations.
Whether and by how much renewable energy development reduces CO2 emissions largely depends on the extent to which increases in renewable energy consumption displace fossil fuel consumption. York3 finds that a one-unit increase in nations’ renewable energy usage is associated with a reduction in fossil fuel usage by less than a quarter of a unit. This may be in part due to the fuel market rebound effect: renewable energy production increases overall energy supply and lowers energy price, which stimulates total energy consumption, including fossil fuel consumption6,7. In high-income nations, many of which have electricity generated from nuclear energy, renewable energy consumption may also displace nuclear energy as opposed to fossil fuels2,18.
Challenging the assumption of Schumpeterian creative destruction in the renewable energy transition, Davidson5 argues that “if left to the vagaries of creative destruction, renewables will not replace fossil fuels until those renewable energy technologies not only achieve price parity with fossil fuels but also become so cheap that they justify the abandonment of the extraordinary levels of sunk costs that continue to be invested in the fossil fuel regime.” More broadly, York19,20 observes a displacement paradox in that introducing newer alternatives to existent technologies or resources does not automatically or necessarily displace the existent but in some cases may simply add to the existing mix.
Underlying renewables’ inadequate effectiveness in decarbonization is that many practices normalized at a societal level, such as personal vehicle-based transportation and the ubiquity of plastics, together with the vast economic and political power of the fossil fuel industry, continue to legitimize the fossil fuel regime despite growth in alternative energy development4,21,22,23. Therefore, Davidson5 argues that in order to achieve the full potential of renewable energies for climate change mitigation, it requires a concurrent “exnovation” of the fossil fuel regime, namely the deliberate and concerted effort to phase out institutions, infrastructure, products, practices, and beliefs that sustain and legitimize the fossil-fuel based energy system. Together, these studies highlight the structural barriers that make it difficult for renewable energies to induce rapid and substantial emission abatement that is necessary to meet the global climate mitigation target.
Next, I discuss the MEP framework and the multidimensionality in the renewable energy-CO2 emissions nexus. A nation’s fossil fuel-burning and CO2-emitting activities can be classified into distinct categories based on characteristics such as supply chain stage and economic sector. Correspondingly, a nation’s CO2 emissions are constituted by multiple structural components24, each is shaped by social, economic, and political economic processes in distinct ways, and has distinct implications for climate mitigation14,25,26,27,28.
To date, however, most cross-national research on the renewable energy-carbon emissions nexus focuses on aggregate national emission outcomes and especially the PBA of emissions, which captures the overall decarbonization effect of renewables on the totality of CO2 emissions—and by extension, the totality of fossil fuel-burning and CO2-emitting activities— that are generated within a nation’s territory. While assessing the overall decarbonization effect is instrumental to understanding the renewable-emissions nexus, the potentially heterogeneous effects of renewables on different structural components of emissions tend to be overlooked. Specifically, renewable energy development’s weak overall decarbonization effect on high-income nations’ PBA does not necessarily mean that it is equally ineffective in mitigating all distinct emission components that constitute the PBA. Instead, renewables might be effective in mitigating only certain emission components but not others. The emission components that cannot be effectively mitigated are the “weak links” that impair the overall decarbonization. Moreover, the relationship between the PBA and renewables does not capture whether developing renewables may induce carbon leakage via offshoring polluting industries, which pertains to how renewables potentially affect emissions embodied in imports.
This study fills the gap by engaging the MEP framework14, which decomposes a nation’s contributions to global emissions into 4 distinct components and examines how broad, economy-wide forces systematically and heterogeneously affect these components: (1) emissions from DOSCA, such as domestic industrial activities that serve domestic consumers; (2) emissions embodied in exports; (3) direct emissions from end-user activities; and (4) emissions embodied in imports. DOSCA emissions, emissions in exports, and emissions in imports are generated by supply chain activities outside the end use phase. Direct emissions from end-user activities are generated by activities such as driving personal vehicles, excluding emissions induced by end-user activities but generated elsewhere in supply chains (e.g., emissions from domestic power plants serving domestic households, which belong to DOSCA emissions). DOSCA emissions, emissions in exports, and direct end user emissions together constitute the PBA. Figure 1 is a conceptual diagram of the MEP framework.
Notes: The figure was originally published in Huang’s study that proposes the MEP framework14.
These 4 emission components are heterogeneously related to broad drivers of emissions, such as economic development and domestic income inequality, and can be viewed as distinct points of decarbonization14,27,29. Their distinctions at the national level are particularly relevant to the renewables-emissions nexus in the cross-national context. For emissions in exports, nations tend to grant preferential treatments—such as carbon tax exemption and free allowance in carbon cap-and-trade programs—to energy-intensive export-oriented industries when implementing energy and carbon regulations, out of the concern that such regulations may increase production costs and undermine the industries’ international competitiveness (esp. against producers in nations with laxer regulations)30,31,32,33,34. These preferential treatments may weaken the motivation for the energy-intensive export industries to reduce fossil fuel consumption and CO2 emissions34,35, thereby limiting how well renewable energy development can decarbonize the export sector.
Among the 4 components, DOSCA emissions and direct end-user emissions are arguably most directly affected by domestic climate and energy policies, and least influenced by foreign policies and global trade dynamics. The main focus of the renewable energy transition has been electricity generation—a main contributor to DOSCA emissions23. Hence, DOSCA emissions are likely the emission component among the 4 that can be most effectively mitigated by renewable energy deployment. In contrast, so far, there have been limited mechanisms through which increased renewable energy consumption can induce a reduction in direct fossil fuel consumption and CO2 emissions by end users. Driving personal vehicles is the main contributor to direct end-user emissions, yet, major types of renewables deployed in road transportation are biofuels like bioethanol and biodiesel, which are more carbon intensive relative to other renewables and hence have limited decarbonization potential7. Biofuels are commonly deployed as blended fuels that contain a large share of fossil fuels (e.g., E10, the most common ethanol blend in the United States, contains 10% ethanol and 90% gasoline). Therefore, the deployment of biofuels in automobile-based transportation may sustain fossil fuel consumption, thus hindering the decarbonization effect of renewables on direct end-user emissions.
Emissions embodied in a nation’s imports are generated by foreign supply chain activities, which are not directly affected by the importing nation’s renewable energy deployment. However, an indirect effect might occur due to carbon leakage via international trade. In the global division of labor, lower-income nations in the Global South undertake substantial export-oriented carbon-intensive production driven by consumer demand of high-income nations in the Global North36,37,38,39,40. A high-income nation’s domestic climate policies might further intensify this dynamic by inadvertently incentivizing its domestic firms to relocate or outsource carbon-intensive operations overseas and then import the products back for consumption, therefore spurring emissions embodied in imports while undermining the effectiveness of the climate mitigation policies34,41,42. As a strategy for climate mitigation, high-income nations’ renewable energy development may potentially cause increases in emissions embodied in their imports. In sum, the distinctions among the 4 emission components allude to the potential heterogeneity in how susceptible these emission components are to the barriers to decarbonization and in how they respond to renewable energy development as a decarbonization strategy. The renewable energy-carbon emissions nexus is likely a multidimensional process consisting of multiple distinct relationships between renewables and these emission components.
Results
Descriptive analysis
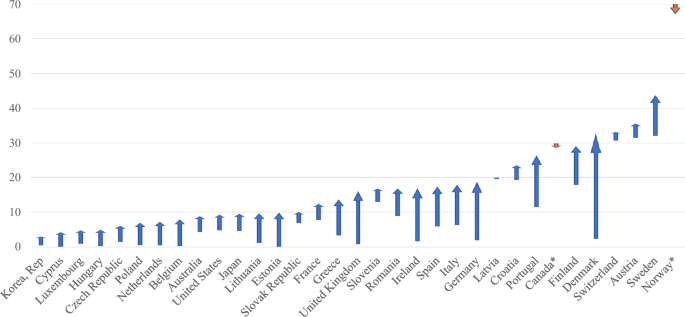
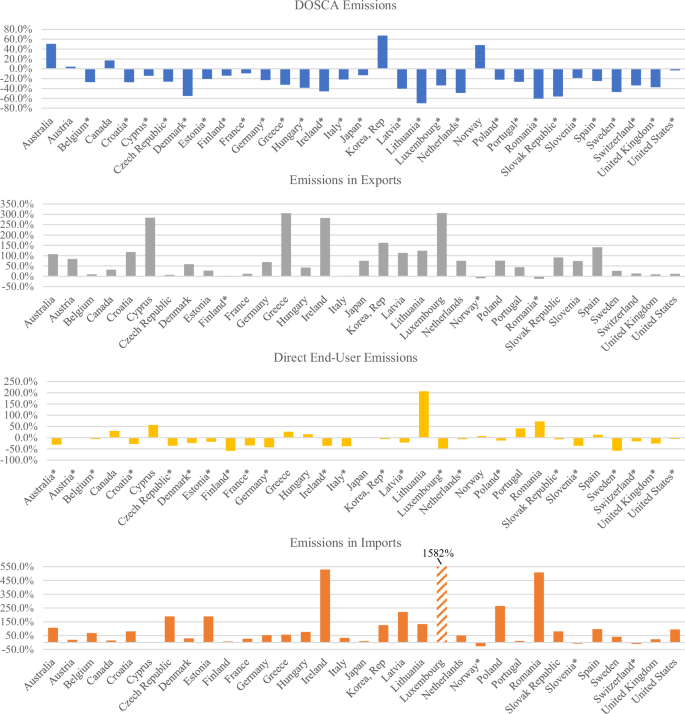
Figure 2 shows that 31 out of the 33 sampled high-income nations increased the share of renewable energy in total primary energy consumption from 1995 to 2019. Figure 3 indicates that 28 nations reduced their DOSCA emissions and 23 reduced direct end-user emissions during this period, whereas a reduction in emissions embodied in exports and emissions in imports is each observed in only 3 nations. It appears that in most sampled nations, an increase in renewable energy consumption occurred concurrently with a decrease in DOSCA emissions and direct end-user emissions during the 1995–2019 period, while emissions embodied in their exports and imports grew substantially.
Baseline multivariate analysis of nations’ PBA
I conduct a baseline analysis of renewables’ relationship with nations’ PBA, reported in Table 1. Elasticity coefficients are reported and flagged for statistical significance based on two-tailed tests. Model 1 includes only the lagged dependent variable, renewable energy, GDP per capita, and total population. Model 2 includes GDP per capita squared, which is not significantly associated with the PBA and thus dropped in the following models. Model 3 includes imports and exports. Model 4 additionally includes manufacturing and urban population. The year 1995 is omitted due to the inclusion of the lagged dependent variable. Models 1 through 4 suggest that, during the 1996–2019 period, renewable energy consumption was negatively and significantly associated with the PBA both in the short and long run, net of the covariates and two-way fixed effects (p < .05). Based on Model 3, a 1% increase in renewable energy consumption is associated with a reduction in the PBA by .018% in the short run, and .126% in the long run.
Model 5 includes the interaction between renewables and year as a single discrete variable. The coefficient for the interaction is negative (p < 0.05), indicating an overall trend that the negative slope of renewables has increased in magnitude over time. Model 6, reported in Table 2, includes interactions between renewables and yearly dummy variables. Statistical significance of the interaction terms suggest that renewables’ slope in each year from 1997 to 2019 does not differ from the main effect in 1996 (p ≥ 0.05), except for 2018. Table 2 also reports the long-run slopes for renewable energy consumption predicting the PBA, which are estimated based on the coefficients and standard errors of the interaction terms, the main effect, and the lagged dependent variable. The long-run slopes remained negative and significant throughout the period (p < 0.05), except for year 2006 (p = 0.0524). In 1996 and 2019, respectively, a 1% increase in renewables was associated with a reduction in the PBA by 0.197% and 0.343% in the long run (p < 0.01). The long-run slope appears to increase in magnitude over time, which is consistent with the significant linear time trend observed in Model 5. In sensitivity analysis (Model 1 in Supplementary Table 1), I estimate interactions between renewables and yearly dummies using year 1997 as the reference category. The coefficients for the interaction terms were negative in the 2011–2012 and 2014–2019 periods (p < 0.05), providing further evidence that renewables’ negative slope generally increases in size over time.
Multivariate analysis of the four emission components
The baseline analysis indicates an overall decarbonization effect of renewable energy development on the PBA, and that the effect has become stronger over time. Is the observed effect, and its enhancement over time, evenly distributed among the 3 components that constitute the PBA? Are certain components less effectively mitigated than others by renewables? Does renewable energy development induce carbon leakages that spur emissions embodied in imports? To answer these questions, I estimate 4-equation SUR models with the 4 emission components being the dependent variables, which are reported in Table 3. In each model, the Breusch-Pagan test indicates that the residuals are significantly correlated across the 4 equations, meeting an assumption of the SUR estimator.
Model 7 includes only renewable energy, lagged dependent variables, total population, GDP per capita, and GDP per capita squared, the last of which is nonsignificant for all 4 emission components and dropped in the following models. Model 8 includes imports and exports, while Model 9 additionally includes manufacturing and urban population. Across Models 7 through 9, renewable energy is negatively associated with DOSCA emissions in both the short and long run (p < 0.05); yet, it is not associated with emissions in exports or direct end-user emissions. Based on Model 8, a 1% increase in renewable energy consumption is associated with a reduction in DOSCA emissions by .037% in the short run and .195% in the long run. Moreover, renewable energy consumption is not positively associated with emissions embodied in imports (p ≥ 0.05), regardless of whether imports (% GDP) is controlled for.
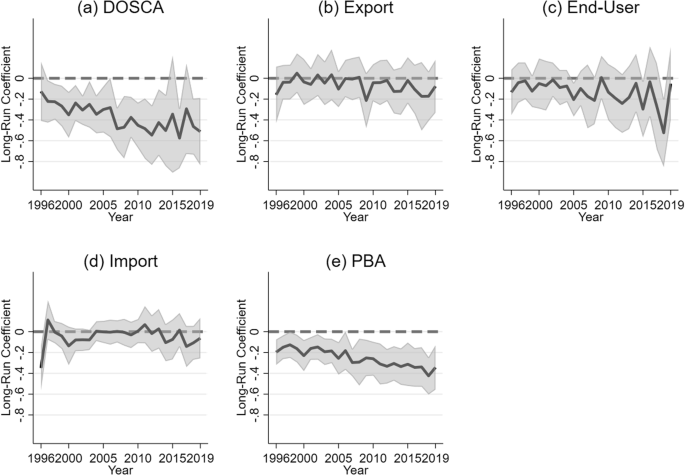
Turning to changes in relationships over time, Model 10 includes the interaction between renewables and year as a discrete variable, which is negative for DOSCA emissions (p < .001) and direct end-user emissions (p < .05), indicating that the slope of renewables trends downward linearly over time for these two emission components. The interaction term is nonsignificant for emissions in exports and emissions in imports. Model 11, reported in Table 4, includes the interactions between renewables and yearly binary variables. Table 4 also reports the long-run slopes for renewables for each year from 1996 to 2019 based on Model 11, which are plotted in Fig. 4 with shaded areas indicating the 95% confidence intervals.
Figure 4(a) suggests that the long-run association between renewables and DOSCA emissions were negative and significant during most of the studied period (p < .05), except for 1996, 2006, 2015, and 2017. Despite some fluctuations, the association generally increased in magnitude over time and especially since 2007, as indicated by the plot and the negative and significant interaction terms for most years since 2007 (p < .05, see Table 4). In 1996, renewable energy consumption was not significantly associated with DOSCA emissions. In 2016, when the magnitude of the association peaked, a 1% increase in renewables was associated with a 0.575% reduction in DOSCA emissions in the long run (p < .001). Figure 4(b) shows that renewable energy’s relationship with emissions in exports remained nonsignificant throughout the period, as the 95% confidence intervals consistently overlap with 0.
Figure 4(c) illustrates that renewable energy’s long-run slope for direct end-user emissions was nonsignificant during most years, except for 2005, 2015 and 2018 when the slope was negative (p < .05). Interannual fluctuations in the magnitude of the slope were substantial, especially since 2014, indicating that a linear time trend might not accurately reflect the temporal variations in the relationship. The negative linear time trend observed in Model 10 might be disproportionally driven by the negative and relatively strong association in 2015 and 2018. Figure 4(d) indicates that renewable energy’s relationship with emissions embodied in imports remained nonsignificant throughout the period (p > = 0.05), except for 1996. For comparison, Fig. 4(e) plots renewables’ negative long-run relationship with the PBA based on Mode 6 in the baseline analysis (Table 2), which appears to increase in magnitude over time and most closely resembles renewables’ relationship with DOSCA emissions plotted in Fig. 4(a).
Among the covariates reported in Table 3, the coefficients for lagged dependent variables are consistently positive and large in size (p < .001), suggesting that they belong to the true data generating process. In other words, the dependent variables are strongly autoregressive. Excluding the lagged dependent variables from the models would lead to omitted variable bias. Based on the short-run coefficients, GDP per capita is only positively associated with emissions in imports but not associated with the other emission components. Total population is positively associated with emissions in exports and emissions in imports but not the other two emission components. Exports (% GDP) is negatively associated with DOSCA emissions and direct end-user emissions, positively associated with emission in exports, and not associated with emissions in imports. Imports (% GDP) is positively associate with emissions in imports and DOSCA emissions (only in Model 8) but not associated with end-user emissions and emissions in exports. Manufacturing (% GDP) and urbanization are not associated with any emission components. I report the long-run coefficients for these covariates in Supplementary Table 6. The direction of the long-run coefficients and their statistical significance levels are substantively similar to those of the short-run coefficients. The nonsignificant coefficients for GDP per capita, population, imports, and exports may be partly attributed to high multicollinearity (see Supplementary Table 9). Manufacturing is excluded in Models 5, 6, 10, and 11— models that include interactions between renewables and year— in order to keep the sample strongly balanced when analyzing changes in the relationship over time. I re-estimate these models while controlling for manufacturing and urban population, and the results remain substantially similar (Models 2 and 3 in Supplementary Table 1, and Models 8 and 9 in Supplementary Table 2).
Discussion
It is crucial to improve the decarbonization effect of renewable energy development as a key strategy of climate mitigation, especially for high-income nations where the decarbonization effect has been found to be relatively inadequate8,9,10,11. This study contributes to this endeavor by engaging the MEP framework to identify the “weak links” in the multidimensional renewable energy-CO2 emissions nexus, filling an important gap in the cross-national research that primarily focuses on how renewable energy development affects nations’ overall CO2 emissions. I identify whether certain structural components of nations’ CO2 emissions are particularly susceptible to the barriers to decarbonization and therefore less effectively mitigated by renewable energy development in high-income nations. I also assess how renewables’ decarbonization effect has changed over time for each emission component, indicative of whether prior strategies on deploying renewable energies have become more effective in overcoming the barriers to decarbonization. Additionally, I investigate whether developing renewable energy exacerbates carbon leakage and spurs emissions in imports.
The results of the statistical analyses indicate a pattern of uneven decarbonization. Developing renewable energy had a weak to moderate overall decarbonization effect on high-income nations’ PBA in the 1996-2019 period. However, this effect is not evenly distributed among the 3 components that constitute the PBA. Instead, renewable energy development is relatively effective in mitigating DOSCA emissions but remains generally ineffective in curbing emissions embodied in exports and direct end-user emissions. This suggests that the observed decarbonization effect of renewables on the PBA is primarily attributed to its effect on DOSCA emissions. Over time, although renewables’ overall decarbonization effect on the PBA has improved, the improvement has been mostly confined to the improved effectiveness in mitigating DOSCA emissions. Meanwhile, renewables’ inability to mitigate emissions embodied in exports has persisted over time, which is particularly concerning given that most high-income nations have seen sizable growth in this emission component during the past two decades. For direct end-user emissions, although renewables’ decarbonization effect appeared to have somewhat improved over time, the effect remained trivial and spotty at best.
It is promising to observe an increasingly stronger decarbonization effect of renewables on the PBA and more specifically on DOSCA emissions, which may be due to the strengthening of policy and private sector support for the renewable energy transition43. The lack of similar suppressive effects on emissions embodied in exports and direct end-user emissions, however, indicates that these two emission components are particularly susceptible to the barriers to renewable energy’s decarbonization effect, which prevent decarbonization from spilling over to these two emission components. Moreover, it appears that over time the barriers have not been overcome for these two emission components by implementing existent strategies of renewable energy development.
For emissions embodied in exports, the ineffective decarbonization by renewables is consistent with the argument that the preferential treatments of energy-intensive export-oriented industries in climate policies diminish the incentive for these industries to reduce fossil fuel consumption and CO2 emissions35,44,45,46. For direct end-user emissions, the mostly nonsignificant effect of renewables may be attributed to the aforementioned lack of effective mechanisms that translate increased renewable energy consumption into reduced direct fossil fuel consumption by end users. These factors may cause the export sectors and end-user activities to be particularly vulnerable to the barriers to decarbonization, including the fuel market rebound effect6,7, the mutual displacement between renewable and nuclear energies2,18, and more broadly the underlying inertia of the fossil fuel regime4,5.
The observed decarbonization effect of renewables on DOSCA emissions is used as a benchmark against which the other emission components are discussed. However, the renewable energy transition has by no means achieved the optimal effectiveness in mitigating DOSCA emissions. Although the effect became greater from 1996 to 2019, it remained inelastic. At its peak, a 1% increase in renewable energy consumption is associated with a reduction in DOSCA emissions by less than 0.6% in the long run, which is consistent with York’s3 observation that each unit increase in renewable energy consumption only displaces fossil fuel consumption by a fraction of a unit. It appears that domestic-oriented industries are also impeded by the barriers to renewables’ decarbonization effect, albeit to a lesser extent than export industries and end-user activities.
The analyses suggest that developing renewable energy in high-income nations does not spur growth in emissions embodied in their imports, which may indicate that renewable energy development does not drive domestic firms to relocate or outsource carbon-intensive operations overseas and then import the products back for consumption. This finding is consistent with prior studies that find domestic climate policies do not induce substantial trade-related carbon leakage, partly due to the preferential treatments given to some energy-intensive domestic-oriented industries with the explicit goal of avoiding carbon leakage34,47. However, carbon leakage might occur more substantially if the preferential treatments are removed48. Additionally, such preferential treatments of energy-intensive domestic-oriented industries likely hamper renewables’ decarbonization effect on DOSCA emissions.
In conclusion, I engage the MEP framework and identify emissions embodied in exports and emissions from direct end-user activities as the weak links of the renewable energy-CO2 emissions nexus in high-income nations. Improving the effectiveness of renewable energy development in mitigating these two emission components is crucial to optimizing renewables’ overall decarbonization effect and, more broadly, to achieving the targets for global climate mitigation. Although this study makes distinct contributions, it has limitations and highlights several avenues for future research. First, a thorough examination of how emissions in exports and direct end-user emissions can be better mitigated is beyond the scope of this study. Future research would do well to investigate what policy instruments can improve renewables’ decarbonization effect on these emission components, potentially drawing from country- and industry-specific case studies. It would also be important to investigate ways to further strengthen renewables’ decarbonization effect on DOSCA emissions. Second, this study only examines high-income nations due to the substantive focus of the research question, as well as the data availability constraints detailed in the “Methods” section. It would be fruitful for future research to examine how renewable energy affects the multiple emission components of middle- and low-income nations, some of which have become major CO2 emitters and energy consumers. Finally, this study demonstrates that the MEP framework, in combination with the more commonly used emission measures, can enable nuanced cross-national analyses on the effectiveness of climate mitigation measures.
Methods
Empirical model
I employ the STIRPAT (Stochastic Impacts by Regression on Population, Affluence, and Technology) model49,50,51, commonly used to examine the effects of anthropogenic drivers on CO2 emissions52,53,54,55,56. The basic STIRPAT model is
where a is the constant that scales the model, population (P) and affluence (A) are two important drivers of impact (I) with b and c being their respective coefficient. Technology is a multifaceted driver encompassing a wide range of factors not captured by population and affluence, and in practice is typically captured by the error term (e) when using the basic STIRPAT model49. Researchers can disaggregate some parts of the technology component by adding other independent variables, including trade openness, urbanization, and of particular interest to this study, renewable energy17,57.
Dependent variables
The baseline analysis uses nations’ PBA of CO2 emissions as the dependent variable. The main analysis focuses on 4 separate dependent variables: (1) CO2 emissions from DOSCA; (2) CO2 emissions embodied in exports; (3) direct CO2 emissions from end-user activities; and (4) CO2 emissions embodied in imports. To obtain the values of these emission variables, I use environmentally-extended multi-regional input-output (EE-MRIO) analysis58, the EE-MRIO tables from the latest version of Exiobase 359,60, and the Python package pymrio61. The EE-MRIO method and Exiobase 3 have been shown by prior studies to be valuable for analyzing environmental impacts of global supply chain activities, including CO2 emissions62,63,64,65,66. When conceptualizing and operationalizing DOSCA emissions, emissions in exports, and emissions in imports, the emissions embodied in internationally traded intermediate goods are allocated to nations where the corresponding final goods are consumed, consistent with the MRIO method67. All dependent variables capture CO2 emissions generated from fossil fuel combustion and are measured in megatons. Full technical details of the EE-MRIO method are reported in at the end of the “Methods” section.
Independent variables
The main independent variable of interest is renewable energy consumption as a percent of total primary energy consumption, acquired from Our World in Data68. This measure accounts for multiple types of renewable energies, including hydroelectric, solar, wind, and biofuel. I use this relative measure of renewable energy consumption because it is aligned with the conceptual focus of the renewable energy transition, which more closely concerns the share of societal energy usage from renewable sources rather than the total amount of renewable energy consumed. This operationalization is consistent with prior cross-national studies on the renewables-emissions nexus8,9.
Consistent with the STIRPAT model, I include gross domestic product (GDP) per capita (constant 2010 U.S. dollars) and total population as additional independent variables. I also include the squared term of GDP per capita to account for a potential quadratic relationship. Trade openness (i.e., the sum of imports and exports as % GDP) is also an important covariate56,69,70. Given that emissions embodied in exports and in imports are two separate dependent variables, I include imports (%GDP) and exports (%GDP) as separate independent variables. In additional models, manufacturing value added (%GDP) is included to account for domestic economic structure, and urban population (%total population) is included to control for the level of urbanization71. I acquire these data from the World Bank’s World Development Indicators Database72.
Sample
The overall panel dataset is strongly balanced and consisted of 825 annual observations from 33 high-income nations in the 25-year period of 1995–2019. Table 5 lists all sampled nations. Due to the inclusion of lagged dependent variables (described below), year 1995 is omitted and the sample size is reduced to 792. In models that include manufacturing value added, the sample size is further reduced to 789 due to missing data. The sample includes all high-income nations, as per World Bank’s country classification73, that have data available for all variables. In particular, the EE-MRIO data that I used to compute the emission variables are available from Exiobase 3 for the 1995–2019 period and for 49 nations and regions, out of which a total of 42 nations also have data available on all other variables. Among these 42 nations, 33 are high-income nations and 9 are non-high-income nations. The analyses focus on the 33 high-income nations, consistent with the conceptual focus of the study. Additionally, the 9 non-high-income nations are excluded in order to avoid potential misleading results from a mixed sample, given that the relationship between renewable energy consumption and CO2 emissions changes substantially across national income levels8,9. Nonetheless, the emission variables of the sampled high-income nations do account for their trade with the rest of the world. For instance, although India is not a sampled nation, the exports from the United States to India are accounted for in the emissions embodied in U.S. exports. The sample includes 9 out of the10 biggest CO2 emitters among high-income nations in terms of the PBA in 2019 based on data from Andrew and Peters13. Tables 6 and 7 report the descriptive statistics and correlation matrix of all variables in their original metrics.
Modeling techniques
For the baseline analysis of the PBA, I estimate a set of dynamic fixed effects regression models that include both time-specific and nation-specific intercepts, in order to account for unobserved heterogeneity that is unique to each year and affects all nations equally, as well as the unobserved heterogeneity that is unique to each nation and invariant across time. I include the lagged dependent variable as a predictor to estimate dynamic models, which accounts for potential autoregression of the emission outcome, helps reduce residual autocorrelation74, and avoids the endogeneity and omitted variable bias if the lagged dependent variable is part of the true data generating process but excluded from the estimated model75,76,77. Including a lagged dependent variable in a fixed effects model introduces the Nickell bias78. However, the bias is unlikely to be substantial because of the relatively long temporal dimension (T = 24).
I estimate country-clustered robust standard errors to correct for residual autocorrelation and heteroskedasticity. Following the STIRPAT model, all non-binary variables are transformed with natural logarithm, and hence the regression coefficients are elasticity coefficients that represent the percentage change in the dependent variable associated with a 1% increase in the independent variables, net of the effects of covariates. The minimal value of renewable energy consumption is 0. Therefore, in the main analysis reported above, I add a constant of 1 to each observation of this variable before transforming it with natural logarithm. In Supplementary Tables 1, 3, and 4 (Models 4 to 7 and 10 to 13) and Supplementary Figures 1 and 2), I report sensitivity analyses where a constant of 0.1 and 0.01, respectively, is added to renewable energy consumption before the log transformation. The results of these models are substantively similar to the main analysis. The general model for the PBA is specified as follows:
where ({{PBA}{CO}2}_{i,t}) is the PBA for nation i at year t; (alpha) is the coefficient for the lagged dependent variable ({{PBACO}2}_{i,t-1}); ({beta }_{1}) through ({beta }_{5}) are short-run coefficients for the independent variables; ({u}_{i}) is the nation-specific intercept for nation i;(,{w}_{t}) is the year-specific intercept for year t; ({e}_{{it}}) is the unique residual for nation i at year t. The long-run coefficients are estimated as ({beta }_{n}/(1-alpha )), where n = 1…5.
I estimate Eqs. (3) and (4) to examine changes over time in the relationship between renewables and the PBA. Equation (3) replaces year-specific intercepts with a single linear discrete variable for year and includes the interaction between renewables and the discrete year variable, a technique that examines whether there is a linear trend in how the relationship changes over time18. The model is specified as below:
Equation (4) includes interaction terms between renewables and yearly binary variables from 1997 to 2019, a technique that examines potential nonlinear variations over time in the relationship56,57,79. The coefficient for the main effect of renewables is the slope for year 1996, the reference category. The coefficients for the interaction terms indicate if the association between renewables and emissions for each subsequent year differs from that of 199680. The model is specified as follows:
The long-run coefficient for renewables in 1996 is estimated as ({beta }_{1}/(1-alpha )). The long-run coefficient for renewables in each year from 1997 to 2019 is estimated as ({{(beta }_{1}+beta }_{n})/(1-alpha )), where n = 29…51.
For the main analysis, I estimate seemingly unrelated regression (SUR) models that are consisted of 4 equations, one for each main dependent variable: DOSCA emissions (DOSCACO2), emissions embodied in exports (EXPCO2), direct end-user emissions (YCO2) and emissions embodied in imports (IMPCO2). The general model also includes nation and year fixed-effects, and lagged dependent variables, specified as follows:
The 4 emission components are interconnected by complex feedback loops including different types of supply chain processes and possible carbon leakage52,81,82,83,84,85, which are not explicitly accounted for in the model. I use the SUR model because it better accounts for these potential underlying relationships among the 4 emission components86, compared to estimating separate models for each emission component. Moreover, the SUR model allows the error terms (({e}_{j,i,t}) for j = 1,2,3,4) to be correlated across the 4 equations, improving the efficiency in estimating parameters in each equation by using the information from all 4 equations86. Nation-clustered robust standard errors are estimated using Stata module suregr87.
Next, I estimate two additional 4-equation SUR models to examine how the associations between renewables and nations’ 4 emission components have changed over time. In the first model, each of the 4 equations excludes year fixed-effects but includes a discrete year variable and its interaction with renewables, similar to Eq. (3) for the PBA. In the second model, each equation includes interactions between renewables and yearly dummy variables, similar to Eq. (4) for the PBA.
Diagnostics
For diagnostics, I first check whether the models achieve an I(0) equation balance, which is required for correct inference based on the t and F statistics88. Based on the Pesaran panel unit root test89,90 and the augmented Dickey–Fuller test91 reported in Supplementary Table 7, I conclude that the dependent variables are stationary and therefore I(0). The independent variables are stationary in either level or first-differenced form. The Pedroni92,93 and Kao94 panel cointegration tests, reported in Supplementary Table 8, suggest that all independent variables cointegrate to reach I(0). For all 5 dependent variables, both sides of the equation reaches an I(0) order of integration, therefore achieving the I(0) equation balance.
I assess multicollinearity by calculating variance inflation factors (VIFs) for independent variables, reported in Supplementary Table 9. The VIF for renewables is consistently below the threshold of 2.5, indicating that extreme multicollinearity does not bias the test of statistical significance for renewables. VIFs greater than 10 are found for imports and exports, as well as for populations, lagged dependent variables, and GDP per capita when lagged independent variables are included, which are at least partly due to the strong bivariate correlation between imports and exports, and between population and each lagged emission variable (Table 7). This, however, does not affect variables with low VIFs such as renewables95.
The Pesaran cross-sectional dependence test indicates that the residuals are strongly cross-sectionally dependent in the models for the PBA, emissions in exports, and direct end-user emissions96,97. Tests of slope homogeneity find significant slope heterogeneity across nations for all emission outcomes98,99. Alternative models such as dynamic common-correlated-effects mean-group models can account for slope heterogeneity and cross-sectional dependence100,101. However, when the time dimension T is smaller than 30, as in the present study, a dynamic two-way fixed effects model used in the main analysis is still preferred because it produces less bias than alternative models even in the presence of slope heterogeneity and cross-sectional dependence76. As part of the sensitivity analyses, I estimate additional models using the xtivdfreg command in Stata102, which follows a general instrumental variable approach that employs principal component analysis on exogeneous covariates to capture unobserved cross-sectional common factors, treats defactored covariates as instrumental variables103,104, and allows for slope heterogeneity using a mean-group estimator. Reported in Supplementary Table 5, these models are separately estimated for each emission outcome. They also exclude the interaction terms between renewables and yearly binary variables to avoid overfitting in mean-group estimation. Different from the main analysis, these models suggest that renewable energy is negatively associated with emissions in exports, though the long-run coefficient is relatively small. The models indicate that among the 4 emission components, renewable energy is negatively and most strongly associated with DOSCA emissions, and not significantly associated with direct end-user emissions or emissions in imports, which is consistent with the main analysis.
EE-MRIO analysis to compute the four components of CO2 emissions
Industry by industry EE-MRIO tables are obtained from Exiobase 3, which provides annual coverage from 1995 to 2019 for 163 harmonized industrial sectors and 49 regions (including nations and rest-of-the-world regions, and hereafter referred to as “regions” following the convention of MRIO analysis). For each year, Exiobase provides a technical coefficient matrix A, which is a 7987 by 7987 matrix (7987 = 163 * 49, and is the number of industry-region pairs); its elements ({a}_{{ij}}^{{RS}})(row indices Ri: R = 1,…,49; i = 1,…,163; column indices Sj: S = 1,…,49; j = 1,…,163) denote the output from industry i in Region R that is required as direct intermediate input for industry j in region S to produce one unit of output. Based on A and the Leontief IO model58,105, a 7987 by 7987 multi-regional Leontief inverse matrix L is computed as below.
where I is a 7987 by 7987 identity matrix. An element of L, denoted as ({l}_{{ij}}^{{RS}}), represents the total output of industry i in region R that is required to satisfy, both directly and indirectly, a one-unit increase in the final demand for the output of industry j in region S.
Next, a 7987 by 49 final demand matrix Y is created based on the final demand data from Exiobase 3; its element ({y}_{j}^{{ST}})(row indices Sj: S = 1,…,49; j = 1,…,163; column index T = 1,…,49) denotes the final demand in region T for product j imported from region S. The T-th column of Y, denoted by vector ({{boldsymbol{y}}}^{T}), represents the final demand in region T for each of the 163 products imported from each of the 49 regions including region T itself.
Then, for each region of final demand T, a partial output matrix ({{boldsymbol{X}}}^{T}) is computed as:
where ({widehat{{{boldsymbol{y}}}^{T}}}) is a 7987 by 7987 matrix obtained by diagonalizing ({{boldsymbol{y}}}^{T}); E is a 7987 by 163 summation matrix created by stacking 49 identity matrices, each sized at 163 by 163, on top of one another. The resulted ({{boldsymbol{X}}}^{T}) is a 7987 by 163 matrix.
Next, all ({{boldsymbol{X}}}^{T}) are assembled side by side in the order of T = 1,…,49 to construct a 7987 by 7987 full output matrix ({boldsymbol{X}}) with elements denoted by ({x}_{{ij}}^{{RT}}) (row indices Ri: R = 1,…,49; i = 1,…,163; column indices Tj: T = 1,…,49; j = 1,…,163). ({x}_{{ij}}^{{RT}}) represents the total output of industry i located in region R that is required to satisfy, both directly and indirectly, the final demand in region T for product j produced anywhere in the world.
A 1 by 7987 of emission intensity coefficient vector s for airborne CO2 emissions from fossil fuel combustion is obtained from the impacts extension of Exiobase 3; each element ({s}_{i}^{R}) represents the CO2 emissions per monetary unit of output of industry i located in region R in a particular year.
A CO2 footprint matrix F is computed as:
where (otimes) refers to the multiplication of s and X without summation along the columns of X. In other words, each element in the n-th row of X is multiplied with the n-th element of s. The resulted F is a 7987 by 7987 matrix, the elements of which are ({f}_{{ij}}^{{RT}},)= ({s}_{i}^{R}{x}_{{ij}}^{{RT}})(row indices Ri: R = 1,…,49; i = 1,…,163; column indices Tj: T = 1,…,49; j = 1,…,163). ({f}_{{ij}}^{{RT}}) represents the total CO2 emissions (in megatons) generated by industry i in region R that is driven, both directly and indirectly, by the final demand in region T for product j produced anywhere in the world.
A region’s four emission components are computed by aggregating selective elements of the footprint matrix F. Emissions generated by DOSCA for region T are computed by aggregating the CO2 emissions generated by all industries i in region T in order to satisfy, both directly and indirectly, its own domestic final demand for all products j, as in:
Emissions embodied in exports of region T are computed by first aggregating the emissions generated by all industries i in region T in order to satisfy the final demand of all regions R for all products j, and then deducting the emissions generated by all industries i in region T in order to satisfy its own domestic final demand for all products j, as in
For direct end-user emissions, Exiobase 3 provides data on the magnitude of CO2 emissions directly generated by 3 categories of final demand activities for each of the 49 regions, in the form of a 1 by 147 vector fY; its elements ({f}_{{Yc}}^{{T}}) (column indices Tc: T = 1,…,49; c = 1,…,3) denote the direct CO2 emissions of final demand category c in region T. The 3 final demand categories are final consumption expenditure of households, final consumption expenditure of non-profit organizations serving households, and final consumption expenditure of general government. The total direct emissions of end-user activities of region T are computed by aggregating the direct CO2 emissions generated by the 3 final demand categories of region T, as in:
Lastly, emissions embodied in imports of region T are computed by first aggregating the emissions generated by all industries i in all regions R in order to satisfy region T’s final demand for all products j, and then deducting the part of emissions generated by all industries i in region T in order to satisfy its own domestic final demand for all products j, as in:
Using these procedures, I compute the four emission components for each of the sampled nations from 1995 to 2019.
Data availability
The dataset used in the current study is available from the corresponding author on reasonable request. This study used the EXIOBASE 3 input-output tables from the EXIOBASE consortium, which can be downloaded from https://zenodo.org/record/5589597#.Y3ffR3bMJEY.
Code availability
The underlying code for this study is not publicly available but may be made available to researchers on reasonable request from the corresponding author.
References
-
UNFCCC. First global stocktake. (2023).
-
Sovacool, B. K., Schmid, P., Stirling, A., Walter, G. & MacKerron, G. Differences in carbon emissions reduction between countries pursuing renewable electricity versus nuclear power. Nat. Energy 5, 928–935 (2020).
-
York, R. Do alternative energy sources displace fossil fuels? Nat. Clim. Chang. 2, 441–443 (2012).
-
York, R. & Bell, S. E. Energy transitions or additions? Energy Res. Soc. Sci. 51, 40–43 (2019).
-
Davidson, D. J. Exnovating for a renewable energy transition. Nat. Energy 4, 254–256 (2019).
-
Balsalobre-Lorente, D., Shahbaz, M., Roubaud, D. & Farhani, S. How economic growth, renewable electricity and natural resources contribute to CO2 emissions? Energy Policy 113, 356–367 (2018).
-
Hill, J., Tajibaeva, L. & Polasky, S. Climate consequences of low-carbon fuels: the United States renewable fuel standard. Energy Policy 97, 351–353 (2016).
-
Thombs, R. P. The paradoxical relationship between renewable energy and economic growth: a cross-national panel study, 1990–2013. J. World-Systems Res. 23, 540–564 (2017).
-
York, R. & McGee, J. A. Does renewable energy development decouple economic growth from CO2 emissions? Socius 3, 1–6 (2017).
-
Bilgili, F., Koçak, E. & Bulut, Ü. The dynamic impact of renewable energy consumption on CO2 emissions: a revisited environmental kuznets curve approach. Renew. Sustain. Energy Rev. 54, 838–845 (2016).
-
Shahnazi, R. & Dehghan Shabani, Z. The effects of renewable energy, spatial spillover of CO2 emissions and economic freedom on CO2 emissions in the EU. Renew. Energy 169, 293–307 (2021).
-
IPCC. Renewable Energy Sources and Climate Change Mitigation. https://doi.org/10.1017/CBO9781139151153 (Cambridge University Press, 2011).
-
Andrew, R. M. & Peters, G. P. The Global Carbon Project’s fossil CO2 emissions dataset. Zenodo https://zenodo.org/records/10562476, https://doi.org/10.5281/zenodo.10562476 (2023).
-
Huang, X. Not all emissions are created equal: multidimensionality in nations’ greenhouse gas emissions and the affluence/emissions nexus. Socius Sociol. Res. a Dyn. World 10, 1–23 (2024).
-
Wang, R., Assenova, V. A. & Hertwich, E. G. Energy system decarbonization and productivity gains reduced the coupling of CO2 emissions and economic growth in 73 countries between 1970 and 2016. One Earth 4, 1614–1624 (2021).
-
Dong, K. et al. CO2 emissions, economic and population growth, and renewable energy: empirical evidence across regions. Energy Econ. 75, 180–192 (2018).
-
Shafiei, S. & Salim, R. A. Non-renewable and renewable energy consumption and CO2 emissions in OECD countries: a comparative analysis. Energy Policy 66, 547–556 (2014).
-
Greiner, P. T., York, R. & McGee, J. A. When are fossil fuels displaced? an exploratory inquiry into the role of nuclear electricity production in the displacement of fossil fuels. Heliyon 8, e08795 (2022).
-
York, R. Ecological paradoxes: William Stanley Jevons and the paperless office. Hum. Ecol. Rev. 13, 143–147 (2006).
-
York, R. Poultry and fish and aquatic invertebrates have not displaced other meat sources. Nat. Sustain. 4, 766–768 (2021).
-
Sicotte, D. M. From cheap ethane to a plastic planet: regulating an industrial global production network. Energy Res. Soc. Sci. 66, 101479 (2020).
-
Sicotte, D. M. & Seamon, J. L. Solving the plastics problem: moving the U.S. from recycling to reduction. Soc. Nat. Resour. 34, 393–402 (2021).
-
Smil, V. Examining energy transitions: a dozen insights based on performance. Energy Res. Soc. Sci. 22, 194–197 (2016).
-
Meng, B., Peters, G. P., Wang, Z. & Li, M. Tracing CO2 emissions in global value chains. Energy Econ. 73, 24–42 (2018).
-
Xu, Y. & Dietzenbacher, E. A structural decomposition analysis of the emissions embodied in trade. Ecol. Econ. 101, 10–20 (2014).
-
Yuan, R., Rodrigues, J. F. D. & Behrens, P. Driving forces of household carbon emissions in China: a spatial decomposition analysis. J. Clean. Prod. 233, 932–945 (2019).
-
Huang, X. Harness the co-benefit and avoid the trade-off: the complex relationship between income inequality and carbon dioxide emissions. Soc. Forces 103, 403–428 (2024).
-
Adua, L., Zhang, K. X. & Clark, B. Seeking a handle on climate change: examining the comparative effectiveness of energy efficiency improvement and renewable energy production in the United States. Glob. Environ. Chang. 70, 102351 (2021).
-
Huang, X. et al. Not all emissions are created equal: multidimensionality in nations’ greenhouse gas emissions and the affluence/emissions nexus. Socius Sociol. Res. a Dyn. World 10, 1–23 (2024).
-
Babiker, M. H., Criqui, P., Ellerman, A. D., Reilly, J. M. & Viguier, L. L. Assessing the impact of carbon tax differentiation in the European Union. Environ. Model. Assess. 8, 187–197 (2003).
-
OECD. Environmentally Related Taxes in OECD Countries: Issues and Strategies. https://www.cbd.int/financial/fiscalenviron/g-fiscaltaxes-oecd.pdf (2001).
-
Böhringer, C. & Rutherford, T. F. Carbon taxes with exemptions in an open economy: a general equilibrium analysis of the German tax initiative. J. Environ. Econ. Manage. 32, 189–203 (1997).
-
Jorgenson, A. K., Clark, R., Kentor, J. & Rieger, A. Networks, stocks, and climate change: a new approach to the study of foreign investment and the environment. Energy Res. Soc. Sci. 87, 102461 (2022).
-
Grubb, M. et al. Carbon Leakage, Consumption, and Trade. Annu. Rev. Environ. Resour. 47, 753–95 (2022).
-
Lin, B. & Li, X. The effect of carbon tax on per capita CO2 emissions. Energy Policy 39, 5137–5146 (2011).
-
Jorgenson, A. K. The sociology of ecologically unequal exchange and carbon dioxide emissions, 1960-2005. Soc. Sci. Res. 41, 242–252 (2012).
-
Givens, J. E., Huang, X. & Jorgenson, A. K. Ecologically unequal exchange: a theory of global environmental injustice. Sociol. Compass 13, e12693 (2019).
-
Prell, C. & Sun, L. Unequal carbon exchanges: understanding pollution embodied in global trade. Environ. Sociol. 1, 256–267 (2015).
-
Prell, C. & Feng, K. Unequal carbon exchanges: the environmental and economic impacts of iconic U.S. consumption items. J. Ind. Ecol. 20, 537–546 (2016).
-
Huang, X. Ecologically unequal exchange, recessions, and climate change: A longitudinal study. Soc. Sci. Res. 73, 1–12 (2018).
-
King, L. C. & van den Bergh, J. C. J. M. Potential carbon leakage under the Paris Agreement. Clim. Change 165, 52 (2021).
-
Aichele, R. & Felbermayr, G. Kyoto and Carbon Leakage: An Empirical Analysis of the Carbon Content of Bilateral Trade. Rev. Econ. Stat. 97, 104–115 (2015).
-
IEA. World Energy Outlook 2022. https://www.iea.org/reports/world-energy-outlook-2022 (2022).
-
OECD. Making taxation and environmental policies mutually reinforcing. Taxation and Environmental Policies https://www.oecd.org/tax/tax-policy/taxationandenvironmentalpolicies.htm.
-
Zhang, Z. X. & Baranzini, A. What do we know about carbon taxes? an inquiry into their impacts on competitiveness and distribution of income. Energy Policy 32, 507–518 (2004).
-
Barker, T., Baylis, S. & Madsen, P. A UK carbon/energy tax. Energy Policy 21, 296–308 (1993).
-
Naegele, H. & Zaklan, A. Does the EU ETS cause carbon leakage in European manufacturing? J. Environ. Econ. Manage. 93, 125–147 (2019).
-
Caron, J. et al. Empirical Evidence And Projections Of Carbon Leakage: Some, But Not Too Much, Probably. in Handbook on Trade Policy and Climate Change (ed. Jacob, M.) 58–75 (Edward Elgar Publishing Ltd, 2022).
-
York, R., Rosa, E. A. & Dietz, T. STIRPAT, IPAT and ImPACT: analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 46, 351–365 (2003).
-
Dietz, T. & Rosa, E. A. Rethinking the environmental impacts of population, affluence and technology. Hum. Ecol. Rev. 1, 277–300 (1994).
-
Dietz, T. & Rosa, E. A. Effects of population and affluence on CO2 emissions. Proc. Natl. Acad. Sci. 94, 175–179 (1997).
-
Dietz, T. Drivers of human stress on the environment in the twenty-first century. Annu. Rev. Environ. Resour. 42, 189–213 (2017).
-
Rosa, E. A., York, R. & Dietz, T. Tracking the anthropogenic drivers of ecological impacts. Ambio 33, 509–512 (2004).
-
Rosa, E. A. & Dietz, T. Human drivers of national greenhouse-gas emissions. Nat. Clim. Chang. 2, 581–586 (2012).
-
Lohwasser, J., Schaffer, A. & Brieden, A. The role of demographic and economic drivers on the environment in traditional and standardized STIRPAT analysis. Ecol. Econ. 178, 106811 (2020).
-
Thombs, R. P. & Huang, X. Uneven decoupling: the economic growth–CO2 emissions relationship in the global North, 1870 to 2014. Sociol. Dev. 5, 410–427 (2019).
-
Thombs, R. P. Has the relationship between non-fossil fuel energy sources and CO2 emissions changed over time? A cross-national study, 2000–2013. Clim. Change 148, 481–490 (2018).
-
Miller, R. E. & Blair, P. D. Input-Output Analysis: Foundations and Extensions. (Cambridge University Press, 2009).
-
Stadler, K. et al. EXIOBASE 3: developing a time series of detailed environmentally extended multi-regional input-output tables. J. Ind. Ecol. 22, 502–515 (2018).
-
Stadler, K. et al. EXIOBASE 3 (Version 3.8.2). Zenodo https://doi.org/10.5281/zenodo.5589597 (2021).
-
Stadler, K. Pymrio – a python based multi-regional input-output analysis toolbox. J. Open Res. Softw. 9, 8 (2021).
-
Bjelle, E. L. et al. Future changes in consumption: the income effect on greenhouse gas emissions. Energy Econ. 95, 105114 (2021).
-
Hertwich, E. G. Increased carbon footprint of materials production driven by rise in investments. Nat. Geosci. 14, 151–155 (2021).
-
Dorninger, C. et al. The effect of industrialization and globalization on domestic land-use: a global resource footprint perspective. Glob. Environ. Chang. 69, 102311 (2021).
-
Bjørn, A. et al. Pursuing necessary reductions in embedded GHG emissions of developed nations: will efficiency improvements and changes in consumption get us there? Glob. Environ. Chang. 52, 314–324 (2018).
-
Tukker, A. et al. Environmental and resource footprints in a global context: Europe’s structural deficit in resource endowments. Glob. Environ. Chang. 40, 171–181 (2016).
-
Peters, G. P., Minx, J. C., Weber, C. L. & Edenhofer, O. Growth in emission transfers via international trade from 1990 to 2008. Proc. Natl. Acad. Sci. 108, 8903–8908 (2011).
-
Ritchie, H., Roser, M. & Rosado, P. Energy. Our World in Data https://ourworldindata.org/energy (2022).
-
Jorgenson, A. K. & Clark, B. Are the economy and the environment decoupling? a comparative international study, 1960–2005. Am. J. Sociol. 118, 1–44 (2012).
-
Shahbaz, M., Nasreen, S., Ahmed, K. & Hammoudeh, S. Trade openness–carbon emissions nexus: The importance of turning points of trade openness for country panels. Energy Econ. 61, 221–232 (2017).
-
Jorgenson, A. K., Auerbach, D. & Clark, B. The (De-) carbonization of urbanization, 1960–2010. Clim. Change 127, 561–575 (2014).
-
World Bank. World Development Indicators. http://data.worldbank.org/data-catalog/world-development-indicators (2022).
-
World Bank. World Bank Country and Lending Groups. https://datahelpdesk.worldbank.org/knowledgebase/articles/906519-world-bank-country-and-lending-groups (2023).
-
Beck, N. & Katz, J. N. Modeling dynamics in time-series-cross-section political economy data. Annu. Rev. Polit. Sci. 14, 331–352 (2011).
-
Pickup, M. Introduction to Time Series Analysis. (Sage, 2015).
-
Thombs, R. P. A Guide to Analyzing Large N, Large T Panel Data. Socius Sociol. Res. a Dyn. World 8, 237802312211176 (2022).
-
Keele, L. & Kelly, N. J. Dynamic models for dynamic theories: the ins and outs of lagged dependent variables. Polit. Anal. 14, 186–205 (2006).
-
Nickell, S. Biases in dynamic models with fixed effects. Econometrica 49, 1417 (1981).
-
Jorgenson, A. K. Economic development and the carbon intensity of human well-being. Nat. Clim. Chang. 4, 186–189 (2014).
-
Allison, P. Fixed Effects Regression Models. (SAGE Publications, 2009).
-
Jarke, J. & Perino, G. Do renewable energy policies reduce carbon emissions? on caps and inter-industry leakage. J. Environ. Econ. Manage. 84, 102–124 (2017).
-
Hu, J., Wood, R., Tukker, A., Boonman, H. & de Boer, B. Global transport emissions in the Swedish carbon footprint. J. Clean. Prod. 226, 210–220 (2019).
-
Liu, J. et al. Complexity of coupled human and natural systems. Science (80-.). 317, 1513–1516 (2007).
-
Davis, S. J., Peters, G. P. & Caldeira, K. The supply chain of CO2 emissions. Proc. Natl. Acad. Sci. USA. 108, 18554–18559 (2011).
-
Peters, G. P. Policy update: managing carbon leakage. Carbon Manag. 1, 35–37 (2010).
-
Srivastava, V. K. & Giles, D. E. A. Seemingly Unrelated Regression Equations Models: Estimation and Inference. (Marcel Dekker, 1987).
-
Kolev, G. I. SUREGR: Stata module to calculate robust, or cluster-robust variance after sureg. Statistical Software Components https://ideas.repec.org/c/boc/bocode/s458938.html (2021).
-
Pickup, M. & Kellstedt, P. M. Balance as a Pre-Estimation Test for Time Series Analysis. Polit. Anal. 1–10 https://doi.org/10.1017/pan.2022.4 (2023).
-
Pesaran, M. H. A simple panel unit root test in the presence of cross-section dependence. J. Appl. Econom. 22, 265–312 (2007).
-
Burdisso, T. & Sangiacomo, M. Panel time series: review of the methodological evolution. Stata J. 16, 424–442 (2016).
-
Maddala, G. S. & Wu, S. A comparative study of unit root tests with panel data and a new simple test. Oxf. Bull. Econ. Stat. 61, 631–652 (1999).
-
Pedroni, P. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxf. Bull. Econ. Stat. 61, 653–670 (1999).
-
Pedroni, P. Panel cointegration: Asymptotic and finite sample properties of pooled time series tests with an application to the PP hypothesis. Econom. Theory 20, 597–625 (2004).
-
Kao, C. Spurious regression and residual-based tests for cointegration in panel data. J. Econom. 90, 1–44 (1999).
-
Allison, P. D. Multiple Regression: A Primer. (Pine Forge Press, 1999).
-
Pesaran, M. H. Testing weak cross-sectional dependence in large panels. Econom. Rev. 34, 1089–1117 (2015).
-
Ditzen, J. XTCD2: Stata Module To Test For Weak Cross Sectional Dependence. https://ideas.repec.org/c/boc/bocode/s458204a.html (2016).
-
Bersvendsen, T. & Ditzen, J. Testing for slope heterogeneity in Stata. Stata J. 21, 1–30 (2021).
-
Pesaran, M. H. & Yamagata, T. Testing slope homogeneity in large panels. J. Econom. 142, 50–93 (2008).
-
Pesaran, M. H. & Smith, R. Estimating long-run relationships from dynamic heterogeneous panels. J. Econom. 68, 79–113 (1995).
-
Pesaran, M. H. Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 74, 967–1012 (2006).
-
Kripfganz, S. & Sarafidis, V. Instrumental-variable estimation of large-T panel-data models with common factors. Stata J. Promot. Commun. Stat. Stata 21, 659–686 (2021).
-
Cui, G., Norkute, M., Sarafidis, V. & Yamagata, T. Two-stage instrumental variable estimation of linear panel data models with interactive effects. SSRN Electron. J. https://doi.org/10.2139/ssrn.3692123 (2020).
-
Norkutė, M., Sarafidis, V., Yamagata, T. & Cui, G. Instrumental variable estimation of dynamic linear panel data models with defactored regressors and a multifactor error structure. J. Econom. 220, 416–446 (2021).
-
Leontief, W. Environmental repercussions and the economic structure: an input-output approach. Rev. Econ. Stat. 52, 262–271 (1970).
Acknowledgements
I would like to thank Andrew Jorgenson, Juliet Schor, Ryan Thombs, Amanda McMillan Lequieu, the Environmental Sociology Working Group at Boston College, as well as the editors and anonymous reviewers for their helpful feedback and comments on the manuscript. I would also like to thank Richard Wood and Arkaitz Usubiaga Liaño for helpful feedback on input-output data analysis. A previous version of this article was presented at the annual meeting of the American Sociological Association in 2023. This study was funded by the Drexel University Faculty Start-Up Fund. The funder played no role in study design, data collection, analysis and interpretation of data, or the writing of this manuscript.
Author information
Authors and Affiliations
Contributions
X.H. conceptualized and designed the study, collected the data, performed the analysis, and wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The author declares no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Huang, X. The multidimensional relationship between renewable energy deployment and carbon dioxide emissions in high-income nations.
npj Clim. Action 3, 107 (2024). https://doi.org/10.1038/s44168-024-00191-5
-
Received: 27 April 2024
-
Accepted: 05 November 2024
-
Published: 20 November 2024
-
DOI: https://doi.org/10.1038/s44168-024-00191-5
Search
RECENT PRESS RELEASES
Related Post