Currently, many educational processes are facing many problems. Problems such as not considering people’s differences, practicing based on weaknesses, finding talents, etc. make many students and students disinterested in education. Using different technologies, artificial intelligence (AI) can inform teachers, professors, and educational administrators about these problems and provide accurate solutions for them^1,2. AI has caused a lot of effects in many industries and fields, and the field of education is one of them. Although many education experts believe that this technology cannot completely eliminate the presence of teachers and lecturers, most of them agree that using AI in the field of education is a very good idea to optimize educational methods^3,4. AI is not only changing the way teachers teach, the technology is also changing the way students learn⁵. For example, AI can design a separate study program for each student and create new ways to access educational materials^6,7. Intelligent education system, automatic scoring and evaluation system⁸, analysis of academic future, curriculum planning⁹, analysis of students’ learning process¹⁰, monitoring student evaluation processes, and recommending educational content¹¹ are among the applications of AI technology in universities and colleges.

In the past years, educational systems around the world have been significantly transformed by AI¹². Due to the evolution of the management system of educational institutions, the need to use AI-based tools in the university is felt more and more. Therefore, platforms based on AI are getting more developed day by day. As is clear from the above discussion, the use of AI in higher learning has numerous advantages including; Personalized learning, automated administrative tasks and Intelligent tutoring systems When implementing AI in higher learning, the following factors should be considered. One of the issues is the effectiveness of the AI-supported educational programs, which can define students’ and institutional performance.

Past studies have examined AI in learning context mostly in the context of predicting students’ performance or evaluating certain learning strategies. Nevertheless, there is a research gap that needs to be filled concerning the factors in the larger environment that affect the quality of AI education. Previous research fails to capture the dynamics of external, internal, and intermediate factors that define the educational context. This research seeks to fill these gaps by developing a framework that encompasses environmental analysis and AI modelling for the improvement of teaching and learning management in the university for AI education. Thus, the present research aims to reveal the factors affecting the quality of AI education by analyzing the external, intermediate, and internal environments and to propose intervention strategies. Also, the proposed AI-based model will be useful in enhancing the field by providing a reliable and effective way of determining the efficiency of AI training programs, which will be useful for the stakeholders in education.

This research proposal presents a new strategy of improving the practice of teaching and management of learning in universities with specific reference to the teaching of AI by adopting macro-environmental analysis and AI modeling. In contrast to prior research that concentrates on forecasting learners’ outcomes or assessing certain instructional approaches, this work encompasses a more comprehensive approach by examining the interactions of extrinsic, transitional, and intrinsic factors that affect the quality of AI education. Furthermore, the proposed work of integrating Capuchin Search Algorithm (CapSA) with Multilayer Perceptron (MLP) for predicting the quality of AI education is a novel contribution to the existing literature. CapSA, a recently developed algorithm based on the foraging behavior of capuchin monkeys, is particularly suitable for searching for solutions within a wide range of solution spaces and is less likely to get trapped into local optima. Through utilizing CapSA in applying modification to the architecture and hyperparameters of the MLP the accuracy of the relationships in the data can be boosted. This kind of synergy between CapSA and MLP enables our model to capture the complex interactions that affect the quality of AI education, and help educational institutions with the insights. The proposed framework is a useful instrument that can be applied by higher education institutions to define the areas of strength and weakness, the usage of the resources, and the efficiency of the education process in AI for the students’ success. This research contributes to the literature by:

• introducing a set of guidelines for assessing the macro-environment of AI education.

• building a new AI model for the prediction of AI education quality.

• presenting quantitative data on the efficiency of the corrective measures suggested in the paper.

• providing directions for enhancing the teaching and learning management in universities in the age of AI.

The article is organized as follows: The introduction was given in the first section. In Sect. 2, the literature is reviewed, followed by presenting the research methodology in Sect. 4. In Sect. 4, the research results were presented and in Sect. 5, the findings are discussed. Finally, in Sect. 6 the conclusion was presented.

In the following, a number of studies related to the research topic are reviewed. Hussain et al. (2019) investigated and predicted students’ problems in learning sessions in a study. For this purpose, they analyzed the data recorded by a technology-enhanced learning using ML algorithm. The results of the evaluation criteria of ML models showed that artificial neural network (ANN), and SVM perform better than other algorithms¹³.

Lau et al. (2019) investigated and predicted student performance in research using ANNs. In this model, they used Levenberg–Marquardt algorithm as the back-propagation learning law. After evaluating the model, the results showed that the neural network (NN) model has acceptable accuracy¹⁴. Sekeroglu et al. (2019) conducted several experiments to predict and classify student performance using ML algorithms. The experiment results demonstrated that the performance of students using ML algorithms can be predicted and by applying pre-processing to raw data before running ML algorithms, their performance classification can be increased¹⁵.

Chen et al. (2020) in a study investigated the effect of AI on the quality of education. The results, while confirming the effectiveness of new AI-based methods, emphasize the ability of ML-based systems in customizing and personalizing educational packages according to students’ needs³. Juan et al. (2020) in a review study investigated and evaluated student performance using ML-based models. The results showed that methods based on ML and ANNs have many capabilities in data analysis and techniques based on AI in the field of student education¹⁶. Hou (2021) proposed a deep neural network (DNN) model in order to evaluate the quality of online teaching and deal with the problems of large-scale datasets. In this proposed model, a support vector regression was used for supervised prediction. Also, large-scale and small-scale data were considered as input to the model in order to evaluate the quality of online teaching. The results of evaluating the proposed model with other shallow models showed that this model is very useful and beneficial for evaluating large-scale data¹⁷.

Fang (2021) proposed a model to evaluate online teaching quality based on SVM algorithm and ML theory. In this research, in order to evaluate the proposed model compared to the surface models, the model’s parameters are tuned and a control experiment was conducted to check the performance of the model. The results of the research showed that the proposed model was effective and efficient in teaching quality evaluation¹⁸.

Namoun and Alshanqiti (2021) in a study investigated the intelligent techniques used to predict student performance. The results showed that regression and supervised ML models are often used to classify students’ performance¹⁹. Ho et al. (2021) investigated the effectiveness of distance learning in higher education. For this purpose, by collecting data on the quality of education during the COVID-19 pandemic and using multiple regression and ML methods, it became clear that the need to review the quality and quantity of distance learning is necessary²⁰.

Okoye et al. (2022) developed an EPDM + ML model for dealing with the student evaluation of teaching and recognizing the factors that affect the recommendation²¹. This model uses text mining and machine learning approach in order to extract sentiments and emotions from the students’ feedback. The research showed that students’ gender and the polarity of the comments they make affect the recommendations. The results of the EPDM + ML model are high accuracy in the prediction of student recommendations, which implies the possibility of enhancing teaching practices.

Yakubu and Abubakar (2022) used machine learning to forecast student academic performance in a Nigerian university²². The researchers used age, gender, high school exam results, region, and CGPA to build the model. The findings showed that female students, the students from high-income regions, and the students with higher high school marks would perform well academically.

Hussain and Khan (2023) dealt with the analysis of student performance at secondary and intermediate levels by applying machine learning algorithms²³. For this purpose, they employ a dataset of the Board of Intermediate & Secondary Education (BISE) Peshawar to train regression and classification models. The paper showed that the machine learning technique was useful and efficient in estimating the students’ grades and marks, which should be beneficial to education.

To improve the prediction of student performance, Asselman et al. (2023) presented a new Performance Factors Analysis (PFA) approach using ensemble learning techniques²⁴. Using Random Forest, AdaBoost, and XGBoost algorithms, they were able to get the better results of prediction accuracy compared to the conventional PFA. This study also implies that the application of machine learning algorithms can enhance the student modeling and the adaptive learning environments.

Ouyang et al. (2023) incorporated an AI performance prediction model to learning analytics for enhancing students’ learning in online engineering courses²⁵. The integrated approach that was adopted in the course was effective in increasing student participation, cooperative learning and satisfaction due to the timely and continuous feedback given to the students. Table 1, summarizes the related works.

According to the literature review, although previous studies have greatly advanced the use of AI in education, there are still some gaps. The literature review is concerned mainly with forecasting students’ performance or assessing particular learning approaches, whereas the evaluation of the university teaching and learning management environment is less researched. This research aims to fill these gaps by providing a new approach based on optimization and machine learning approached.

This section of the article proposes strategies to address the challenges about applications of AI in universities, attempting to tackle them from two different perspectives. Initially, by employing a macro-environment segmentation method, corrective actions and their impacts on the management of education and learning in universities are examined within the context of AI education. Subsequently, an effective strategy, grounded in ML techniques, is presented to develop high-quality AI educational programs in higher education.

Corrective actions in university education and learning management, within the context of AI education, based on macro-environment segmentation

This section proposes a set of corrective actions in university education and learning management within the context of AI education, based on macro-environment segmentation. According to this research, the macro environment of university teaching and learning is divided into three parts: the external environment, the intermediate environment, and the internal environment. In the external environment, actions such as enacting supportive laws and regulations for AI education, collaborating with relevant industries and institutions, and utilizing external resources for the advancement of AI education are undertaken. In the intermediate environment, actions like establishing an appropriate management structure, developing human resources, and employing new teaching and learning technologies are carried out. Finally, within the internal environment, actions such as designing and offering AI-based educational programs, developing AI-based teaching and learning methods, and assessing the effectiveness of AI education are performed.

External environment

The external environment encompasses factors that are beyond the control of universities. These factors can influence university teaching and learning. Corrective actions in the external environment can aid in creating conducive conditions for the advancement of AI education in universities. These actions can be undertaken by governments, relevant industries and institutions, and the universities themselves. Following are the necessary corrective actions in the external environment listed to enhance university teaching and learning in the context of AI education:

• Establishing laws and regulations to support AI education: Governments can assist in the development of this field in universities by establishing supportive laws and regulations for AI education. These laws and regulations may include the following:

• Financial support for universities to develop AI education: Governments can support the development of AI education in universities by allocating government funds. These funds can be used to cover financial expenses, provide human resources, and acquire necessary technologies for the advancement of AI education.

• Facilitating collaboration between universities and related industries and institutions: Governments can support the development of AI education in universities by facilitating collaboration between universities and related industries and institutions. These facilitations may include the following:

  • Establishing laws and regulations to support collaboration between universities and related industries and institutions.

  • Providing financial and tax incentives to companies that collaborate with universities.

• Establishing educational standards for AI education: Governments can ensure the quality of AI education in universities by establishing educational standards. These standards may include the following:

  • Determining the necessary educational content for AI education.

  • Determining the evaluation methods for AI education.

• Collaboration with related industries and institutions: Universities can benefit from the knowledge and experience of these organizations in developing AI education through collaboration. These collaborations can lead to the formation of joint educational programs, conducting joint research, and providing financial resources for the development of AI education.

• Utilizing external resources for the development of AI education: Universities can make use of external resources, such as government grants, private sector grants, and grants from international organizations, to develop AI education. These resources can be used to cover financial expenses, provide human resources, and acquire necessary technologies for the development of AI education.

Intermediate environment

The intermediate environment includes factors that are within universities but outside the direct control of managers and education and learning experts. These factors can influence teaching and learning in universities. Corrective actions in the intermediate environment can help establish an appropriate structure and conditions for the development of AI education in universities. The corrective actions in the intermediate environment include:

• Establishing an appropriate management structure: Universities should establish an appropriate management structure for the development of AI education. This structure should include the following:

  • A management unit or center responsible for AI education.

  • A policy council for AI education.

  • An expert team for the development of AI education.

• Development of human resources: Universities should undertake necessary actions to develop human resources specialized in AI. These actions may include the following:

  • Conducting training courses for university staff.

  • Attracting and hiring AI specialists.

  • Creating job opportunities for AI specialists at the university.

• Utilizing new teaching and learning technologies: Universities should utilize new teaching and learning technologies for the development of AI education. These technologies may include things like ML, DL, virtual reality, augmented reality, and so on.

Internal environment

The internal environment includes factors that are within universities and under the direct control of managers and education and learning experts. These factors can influence teaching and learning in universities. Corrective actions in the internal environment can contribute directly to the development of AI education in universities. The corrective actions in the university’s internal environment include:

• Designing and offering AI-based educational programs: Universities should design and offer educational programs based on AI. These programs should fulfill the needs of students and society.

• Development of AI-based teaching and learning methods: Universities should develop teaching and learning methods based on AI. These methods should facilitate active and collaborative learning among students.

• Evaluating the effectiveness of AI education: Universities should evaluate the effectiveness of AI education. These evaluations can contribute to improving the quality of AI education.

In summary, corrective actions in the macro, intermediate, and internal environments can aid in the development of AI education in universities. Considering the above, it can be inferred that employing efficient and precise strategies for evaluating the quality and effectiveness of AI educational programs is one of the primary requirements at various levels. Implementing this process in traditional ways can be time-consuming and complex. However, by utilizing AI techniques, this task can be accomplished more desirably. The next section presents a strategy based on AI techniques to achieve this goal.

Proposed strategy for evaluating the quality of AI training programs in higher education

In this section, a new strategy is proposed for quality evaluation of AI education programs in higher education. In this regard, the dataset used for designing this model is described first, followed by the presentation of the steps of the proposed strategy.

Data

In this research, a dataset containing information related to AI educational programs at higher education levels was utilized. This data was collected through in-person AI training classes from various technical and engineering faculties. During the data collection process, 188 questionnaires were distributed among the respondents in the target population. After the data collection, the accuracy and completeness of the provided information were verified. All the questionnaires were anonymous, without any personal or identity information. This study was conducted following ethical principles for research involving human subjects. This study did not involve human subjects research as defined by Belmont Report. Data was collected through a voluntary anonymous questionnaire that did not pose any risks beyond those encountered in daily life. Informed consent was obtained from all subjects and/or their legal guardian(s). No identifiable data was collected through questionnaires. Additionally, all dataset instances were anonymized and the attributes were encoded; therefore, none of the participants could be identified through the data. None of the questionnaires contained any invalid information. Conversely, 8 questionnaires contained at least one unanswered question, which were discarded due to the presence of missing values in the analysis process. Therefore, the total number of samples in the dataset used in this research amounts to 180. All the questionnaires were evaluated by three experts, and the quality of the educational program was determined as a numerical variable ranging from zero (worst) to 100 (best). Ultimately, an averaging strategy was used to determine the final score for each sample. The standard deviation of the scores determined by the experts is 2.66, which validates the collected information.

The list of indicators collected through questionnaires is presented in Table 2. The dataset listed in this table encompasses three general categories, each of which could potentially be related to the quality of the educational program. Consequently, this research aims to evaluate the AI education quality using (a subset of) the 14 indicators that have been listed as Table 2.

Proposed quality evaluation algorithm

The proposed algorithm for the AI education quality evaluation in higher education utilizes a combination of optimization techniques and ML. In this approach, the optimization technique is initially used for identifying the indicators associated with the quality of AI training. Subsequently, an optimally structured artificial neural network (ANN) is utilized for prediction. This algorithm can be broken down into the following steps:

1. 1.

   Data Pre-processing.

2. 2.

   Feature Selection based on the Capuchin Search Algorithm (CapSA).

3. 3.

   Quality Prediction based on ANN and CapSA.

The rest of this section is devoted to the description of each of the above steps.

Data preprocessing

The data preprocessing stage is the initial phase of the proposed model and is utilized to prepare the database for processing in subsequent stages. This stage comprises two steps: value conversion and normalization. To this end, all nominal features are first converted into numerical values. Specifically, for each nominal feature, a unique list of all its nominal values is initially prepared. In ranked features, the unique values obtained are sorted based on rank, and in discrete nominal features, this list is sorted in ascending order based on the frequency of the value in that feature. Then, the nominal value is replaced by a natural number corresponding to its position in the sorted list. By doing this, all the features of the dataset are converted into a numerical format. At the end of the pre-processing step, all features are mapped to the range [0, 1] based on the following relationship:

Where, (:overrightarrowx) represents the input feature vector and (:overrightarrowN_i) represents the corresponding normalization vector. Also, min and max are the minimum and maximum functions for the feature vector, respectively.

Feature selection using CapSA

After normalizing the features of the database, the process of feature selection and data dimension reduction is carried out. This algorithm aims to reduce the dimensions of the features, thereby increasing processing speed and reducing the error rate in evaluating the quality of AI training. The CapSA algorithm is utilized to achieve this goal. CapSA is a proven and fast meta – heuristic optimization algorithm that is applicable in feature selection. It is capable of both global search and local fine-tuning, does not get trapped into local optima and is fast-converging to good solutions. Compared with other algorithms such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO), CapSA is easier to implement, faster and less likely to converge into local optima. First, CapSA increases the model’s accuracy and decreases overfitting by choosing appropriate features, which also increases model interpretability. Subsequently, the structure of the response vector and the objectives defined for the optimization algorithm are first explained, followed by a description of the feature selection steps using CapSA.

In the proposed method, the number of optimization variables corresponds to the number of features present in the database (Table 2), which is equal to 14. In other words, each solution vector of the optimization algorithm is of length 14. CapSA should be capable of determining the selection or non-selection of a feature via the response vector. In this way, each solution vector can be viewed as a binary string where each existing feature is assigned a position in the response vector of the optimization algorithm. Each position can have a value of 0 or 1. If a position has a value of 0, that feature is not selected in the current solution, and if it has a value of 1, the feature corresponding to the current position is considered as the selected feature.

Optimization objectives can be considered the most crucial part of an optimization algorithm. In the proposed method, the following two objectives are utilized to assess the quality or fitness of solution vectors in CapSA:

A) Maximizing the average correlation of the selected features with the target variable: The more a feature correlates with the target variable of the problem, the more significant that feature becomes. In other words, it becomes easier to predict the change in the target based on it. For this reason, maximizing the correlation of the selected features with the target variable is considered as the first objective in the optimization algorithm. This objective criterion is described in Eq. (2):

Where, S represents the set of features selected in the current response and (:left|Sright|) represents the number of these features. Also, T describes the target variable and (:corr(i,T))is the correlation evaluation function between the selected feature i and the target variable.

B) Minimizing the average correlation of selected features with each other: A feature is suitable for selection if it can provide new information compared to other selected features. Features that have highly correlated values exhibit similar patterns, and it is not appropriate to select them as descriptive features of the data. For this reason, minimizing the correlation of selected features is considered as the second objective of CapSA. This objective can be described in Eq. (3):

Since the two aforementioned objectives are incompatible with each other (the first objective is defined as a maximization problem and the second objective is defined as a minimization problem), they need to be harmonized in the optimization algorithm. Therefore, they are combined in the form of the following fitness function:

Thus, the goal of the feature selection algorithm in the proposed approach is to identify features that can minimize the above relationship. The proposed algorithm, which aims to select the most relevant features to the quality of AI training using CapSA, is as follows:

Step 1) Determine the initial population randomly based on the boundaries set for each optimization variable.

Step 2) Determine the quality of each capuchin (solution) using Eq. (4).

Step 3) Set the initial velocity of each capuchin agent.

Step 4) Select half of the Capuchin population randomly as leaders, and designate the rest as follower Capuchins.

Step 5) If the number of iterations of the algorithm has reached the maximum value of G, proceed to step 13. If not, repeat the following steps:

Step 6) Calculate the CapSA lifetime parameter using Eq. (5):

Where, g represents the current iteration number, and the parameters (:beta:_0), (:beta:_1), and (:beta:_2) are the coefficients of CapSA lifetime.

Step 7) Repeat the following steps for each Capuchin agent (both leader and follower) like i:

Step 8) If i is a Capuchin leader, update its velocity based on Eq. (6):

Where, j represents the dimensions of the problem, and (:v_j^i) represents the velocity of capuchin i in dimension j. (:x_j^i) indicates the position of capuchin i for the jth variable, and(:x_best_j^i) describes the best position of capuchin i for the jth variable from the beginning until now. Also, (:r_1) and(:r_2) are two random numbers in the interval [0, 1]. Finally, � is the parameter that influences the previous velocity.

Step 9) Update the new positions of the leader Capuchins based on their velocity and movement pattern.

Step 10) Update the new positions of the follower Capuchins based on their velocity and the position of the leader.

Step 11) Determine the quality of the population members using Eq. (4).

Step 12) If the position of the entire population is updated, proceed to step 5; else, go to step 7.

Step 13) Return the solution with the best quality value as the set of selected features.

After executing the above steps, a set, such as X, is selected as significant features for the quality of AI training in higher education. This set is then used as the input for the third step of the proposed method. It should be noted that while implementing CapSA for feature selection, the population size and umber of iterations were set as 50 and 100, respectively. Also, the parameters of CapSA lifetime: (:beta:_0), (:beta:_1), and (:beta:_2) (in Eq. 5) were considered as 2, 21, and 2, respectively. Additionally, the parameter � for influencing the previous velocity in Eq. 6 was set at 0.7.

Quality prediction based on ANN and CapSA

After identifying the set of indicators that impact the quality of AI education, the final phase of the presented approach attempts to predict the target variable based on these indicators. The current research is an effort to model the relationship among the selected features and the target (quality of education) using ANNs. To achieve an accurate prediction model, attention must be given to the problem of optimally configuring the MLP model. The use of many neurons and layers in the MLP model can increase the complexity of the model, and conversely, using models with less complexity can lead to a decrease in prediction accuracy. Also, conventional training algorithms for adjusting the weight values of NNs cannot guarantee achieving the highest prediction accuracy. To address these challenges, CapSA is used in the proposed method to optimize the configuration of the MLP model and its training. The proposed CapSA-MLP hybrid model provides an effective solution for the quality prediction of AI education. As a result, CapSA adjusts MLP architecture and weight vectors enhancing the model’s performance of learning patterns in a data set. In general, MLPs are appropriate for nonlinear mappings and can be used for regression as well as for classification. As the result, the proposed hybrid model built based on the CapSA and MLP could provide a more accurate and reliable model for the quality prediction of AI education.

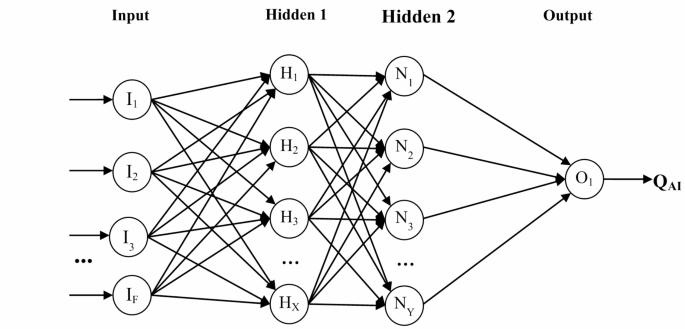
In the proposed method, CapSA replaces the conventional training algorithms for MLPs. This optimization model not only adjusts the configuration of the MLP model’s hidden layers but also strives to determine the optimal weight vector for the NN. It does this by defining training performance, as the objective function. Figure 1 illustrates the structure of the NN that the proposed method uses to predict the quality of AI training.

Structure of the NN employed for predicting the AI education quality.

Full size image

According to Fig. 1, the proposed NN comprises an input layer, two hidden layers, and an output layer. The input layer is populated with the features selected in the previous phase. CapSA determines the number of neurons in the first and second hidden layers. Consequently, the proposed MLP structure lacks a static architecture. On the other hand, the activation functions of these two hidden layers are set as logarithmic and linear sigmoid, respectively. Finally, the output layer consists of a neuron, the value of which indicates the predicted score for the input sample. Each neuron in this NN receives a number of weighted inputs, depicted as directional vectors in Fig. 1. In addition, each neuron possesses a bias value, omitted from the figure for simplicity. Under these conditions, the output of each neuron, transferred to the neurons of the subsequent layer, is formulated as follows:

Where, (:x_n) and (:w_n) denote the input value and weight of the n_th neuron, respectively, and (:b_i) represents the bias value of this neuron. Also, (:N_i) indicates the number of inputs of the i_th neuron and (:G(.)) defines the activation function. As previously mentioned, CapSA is utilized to determine the number of neurons in the hidden layers and to fine-tune the weight vector of this NN. The optimization steps in this phase mirror the process outlined in the second step (feature selection). The distinction in this phase is that a different approach is employed to encode the solution vector and assess fitness. Consequently, the structure of the response vector and the criteria for evaluating suitability are elucidated in the following.

The response vector (capuchin) in the capuchin search algorithm, utilized in the presented approach, dictates the topology of the MLP, and also its weights/biases vector. Consequently, each response vector in CapSA is composed of 2 interconnected parts. The first part is defined for determining the size of hidden layers in NN, while the second part of solution defines its weight/bias vector, and corresponds to the topology established in the first part. Consequently, the capuchins in this step possess a variable length. Given that the number of states for the NN topology can be infinite, a range of 0 to 15 neurons is envisaged for each hidden layer in the aforementioned network. Therefore, each entry in the first part of the response vector is a natural number in the range of 0 to 15, and if a layer is defined with no neurons (0), that layer is eliminated. It’s worth noting that in the first part of each capuchin only specifies the size of hidden layers (not input or output layers).

The length of the second part of the solution vector is dictated by the topology established in the first part. For a NN with I input neurons, H₁ neurons in the first hidden layer, H₂ neurons in the second hidden layer, and P output neurons, the length of the second part of each solution vector in CapSA corresponds to:

Where, (:H_1times:left(I+1right)) represents the number of weight values between the neurons of the input layer and the first hidden layer, in addition to the bias of the first hidden layer. The value of (:H_2times:left(H_1+1right)) denotes the number of weights between the first and second hidden layers, along with the bias of the second hidden layer. Finally, (:Ptimes:(H_2+1))illustrates the number of weights between the last two layers, as well as the bias of the output layer. Consequently, the length of the second part of each solution vector in the optimization algorithm equates to L. In this vector, the value of the weight and bias is represented as a real value within interval [-1, + 1]. In other words, each optimization variable in the second part of the chromosome is characterized as a real variable with search boundaries of [-1, + 1].

The first population of CapSA was generated randomly. The NN produces outputs for the training instances after the weights have been determined by the solution. These outputs are then matched with the ground-truth values of the target and based on that, the NN’s performance (training quality) is measured. Subsequently, the Mean Absolute Error (MAE) criterion is utilized to assess both the NN’s training quality and the optimality of the response. Consequently, the objective function of the CapSA is formulated by Eq. (9):

Where, N denotes the number of training instances and T_i indicates the actual value for the target of i_th training instance. Also, Zi corresponds to the output generated by the NN for the i_th training sample. As previously mentioned, the optimization steps of the MLP model by CapSA in this phase mirror the process outlined in the second step (feature selection), thus the repetition of these contents is foregone. Upon determining the NN with the optimal topology and weight vector that can minimize Eq. (9), this NN is employed to predict the quality of training in new samples. In should be noted that in this phase, the CapSA was implemented using the parameter setting same as the values considered for feature selection.

In this section, the research results are reviewed and analyzed. MATLAB 2020a software was used for implementation. In the experiments, a 10-fold cross-validation approach was used to evaluate the efficiency of the models in prediction. This strategy divides the dataset instances into two subsets in each iteration: 90% of the data are used for training and the remaining 10% (unseen instances) for testing the model. After 10 iterations, all of the instances are employed for testing model. This strategy in addition to efficiently handling scenarios with limited instances, can be used to examine the generalizability of the prediction models, and therefore was chosen as the scenario of the experiments.

At the end of each iteration of the experiments, the predicted values for test instances are contrasted with the actual values using various measures such as Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), R², Pearson Linear Correlation Coefficient (PLCC), Spearmans Rank Order Correlation Coefficient (SROCC), and Concordance Correlation Coefficient (CCC).

The RMSE is a metric used to measure the average of the squares of the errors between predicted and actual values, providing a single number to summarize the performance of a model in predicting continuous numeric outcomes. RMSE is measured as follows:

Where, N denotes the number of the data samples. (:Y_i) represents the label vector of the i-th sample, and (:widehattexty_textl) is the corresponding predictions of the sample using the learning model.

MAPE calculates the average absolute percentage error between predicted values and actual values over a given dataset. The equation for MAPE is:

Where (:y_i) is the product’s actual value, (:widehaty_i) is the forecast value, (:N) is total number of observations. The CCC measure, evaluates the concordance between predicted and actual values, ascertaining if the model’s predictions are consistent in both direction and scale, and is defined as follows:

Where, (:sigma:_i^2) and (:mu:_i) are the variance and mean of the measurements made by observer i and (:sigma:_ij) is the covariance between the measurements from observers i and j. The PLCC quantifies the linear association between anticipated and actual values, ranging from − 1 to 1, where 1 signifies a perfect positive correlation, -1 a perfect negative correlation, and 0 shows no correlation. PLCC is defined as follows:

The SROCC assesses the model’s responsiveness to relative variations between actual and predicted values, rendering it appropriate for non-normally distributed data or data containing outliers. The definition of SROCC is as follows:

R-squared denotes the proportion of variation in actual values elucidated by the model, ranging from 0 to 1; a larger number signifies superior model efficacy in forecasting crime occurrences.

Where, SSR is sum of squared regression also known as variation explained by the model. SST is total variation in the data also known as sum of squared total. (:y_i:)is the y value for observation i. (:stackrel-y:)is the mean of y value. (:widehaty) is predicted value of y for observation i.

Based on the mentioned metrics, the proposed method was compared with the following cases:

• Proposed (no FS): This scenario refers to the case that the feature selection step in the proposed approach is omitted and predictions are made based on all input features. Comparing the proposed approach with this scenario can demonstrate the effectiveness of the CapSA-based feature selection algorithm in improving the performance of predictions.

• ANN(LM): In this scenario, after selecting features using the proposed method, a simple ANN is trained by the conventional Levenberg-Marquardt algorithm for making predictions.

• ANN(SCG): In this scenario, after selecting features using the proposed method, an ANN is trained by the scaled conjugate gradient algorithm for making predictions. Comparing the proposed approach with the LM and SCG cases, can demonstrate the difference between the proposed hybrid CapSA-MLP approach with the conventional training algorithms.

• Hou¹⁷: This approach is one of the recent models which uses DNNs for prediction and is efficiently usable for analyzing small- to- large-scale datasets. Comparing the proposed model with this approach can provide an insight about performance difference between our CapSA-MLP and deep learning models.

• Fang¹⁸: This model employs an SVM for prediction. Including this recent model in the comparisons can reveal the difference between the performance of the proposed approach with the classical machine learning models.

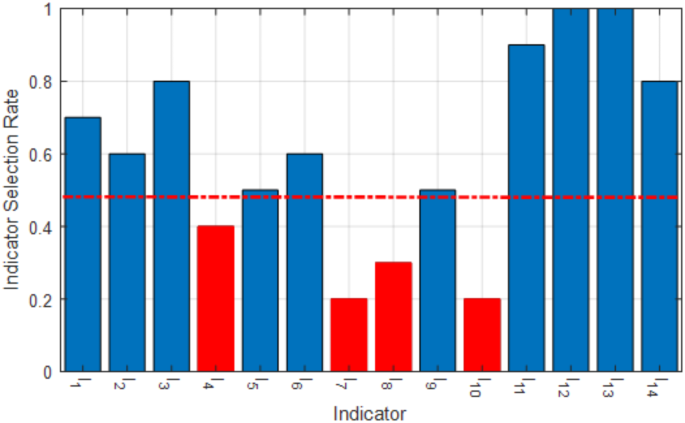
As mentioned earlier, feature selection was done using the CapSA algorithm. The purpose of the feature selection algorithm in the proposed method is to determine a set of features with the lowest provided index values based on Eq. (4). Figure 2 shows the indicator selection rate values based on the CapSA algorithm in 10 repetitions. The indicators that were selected in at least half of the iterations were selected as the indicators affecting the AI education quality.

Feature selection using CapSA algorithm.

Full size image

According to Fig. 2, the selection rate values of features I4, I7, I8 and I10 have rates less than 0.5. Therefore, these four features were not selected as the most relevant indicators. Also, features I12 and I13, which respectively represent “Rate of student participation in doing assignments outside of class� and “Average student evaluation score during the academic term� were selected as the indicators affecting the AI education quality.

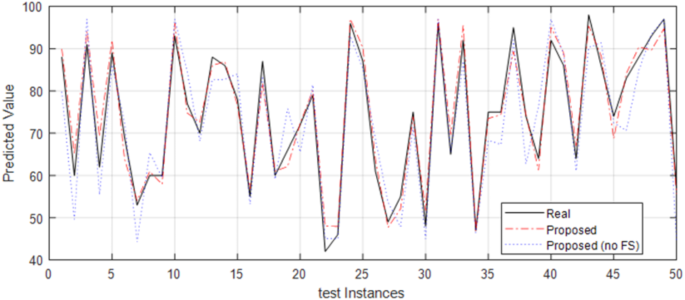
Figure 3 shows the predicted values of the target variable by the proposed approach for 50 test instances based on the CapSA algorithm (Proposed) and without using the feature selection method (Proposed (no FS)). As it is clear from this figure, the proposed method has a better fit with the real values, compared to the case that all features are employed for predictions. The predictions made based on the selected features shows a smaller difference with the actual values which leads to lower error and improved efficiency. This is an example of positive influence of the proposed feature selection approach on the performance of the prediction model. In the following, we will compare the proposed method with other approaches based on various metrics.

Time series of predicted values based on Proposed and Proposed (no FS) methods based on test dataset.

Full size image

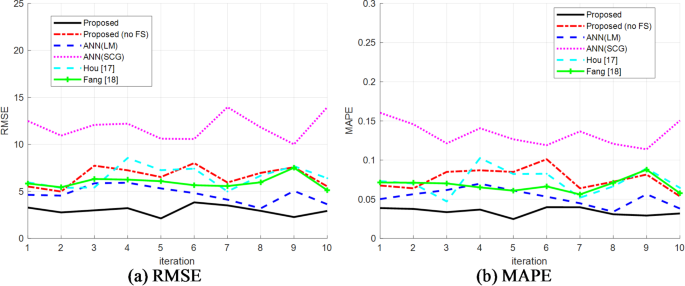
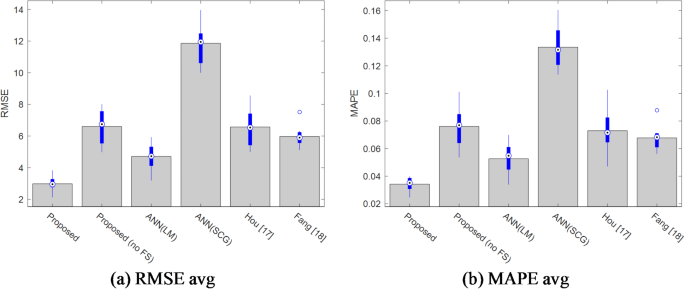
Figure 4 shows the RMSE and MAPE values of all models in predicting education quality during 10 folds of cross validation. According to Fig. 4, the values of RMSE (in Fig. 4a) and MAPE (in Fig. 4b) related to the Proposed model in all iterations are lower than the corresponding values in other models. In other words, the proposed model has the lowest error in predicting the target variable (quality of education). On the other hand, the ANN (SCG) model has the highest error values in all repetitions and, as a result, the lowest accuracy compared to the others.

RMSE and MAPE values of models in prediction during 10 folds of cross validation.

Full size image

Figure 5 shows the average values and box plot for the RMSE and MAPE variations in all models. In this figure, the average of RMSE and MAPE are illustrated as gray bars, while the boxplot of these measures’ variations is depicted as blue bars. The white dots demonstrate the median of the errors. This figure demonstrates the effectiveness of our approach in reducing the prediction error. According to these results, the introduced model leads to smaller RMSE and MAPE values; and at the same time produces smaller ranges of these error values which proves the reliability of the predictions made by this model. After this model, ANN(LM), Fang, Hau, proposed (no FS) and ANN (SCG) models have the highest accuracy in the next ranks of the model.

The average values and box plot for the RMSE and MAPE variations in all models.

Full size image

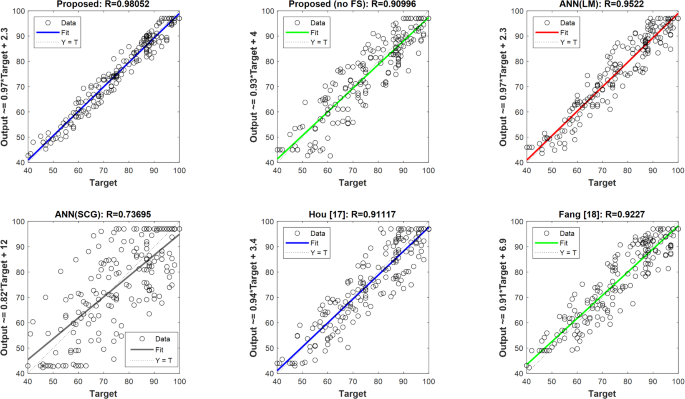
In Fig. 6, observation-prediction regression plots of all models are shown along with their correlation coefficient (R) values. Also, the values predicted by the models along with the equation of the fitting line are shown along the vertical axis of the graphs. According to this figure, it is clear that the scatter of data around the fitting line in the proposed model is less than other models. The R coefficient value of this model is equal to 0.98052, which is higher than the corresponding values in other models. This means that the proposed model has been able to predict the observed values more accurately. On the other hand, as it is clear from this figure, the ANN(SCG) model has the highest data dispersion and as a result has the lowest accuracy compared to others.

The Observation-Prediction plots.

Full size image

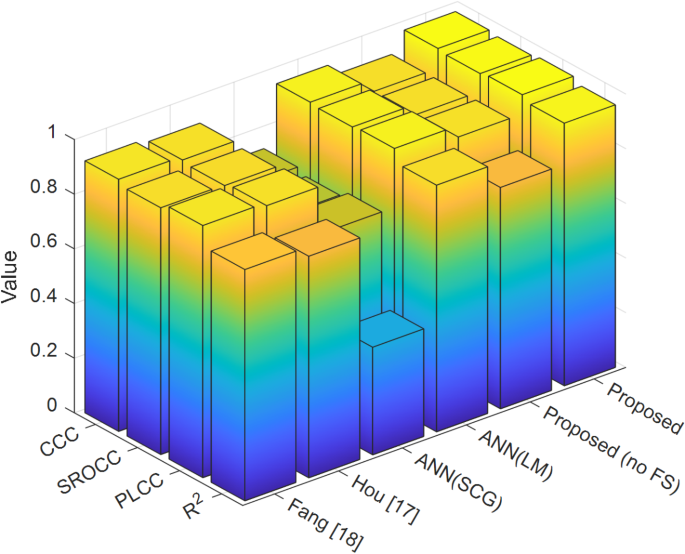
Figure 7 shows the values of CCC, SROCC, PLCC and R² indices for all models. According to this figure, it can be seen that Proposed and ANN(SCG) models have the highest and lowest values of the mentioned indicators, respectively, compared to others. As a result, these indicators confirm that the Proposed model has the highest accuracy and the ANN(SCG) model has the lowest accuracy in predicting the target variable.

Values of CCC, SROCC, PLCC and R² indices for all models.

Full size image

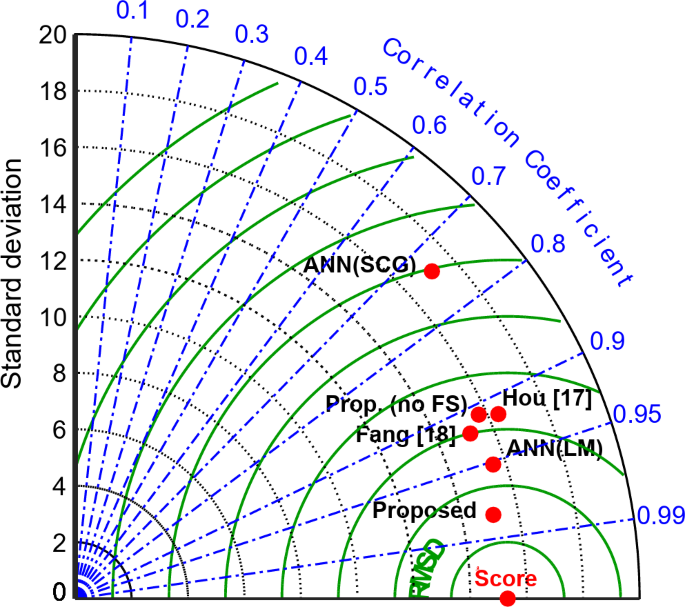
In Fig. 8, the Taylor diagram related to all models is shown. In this diagram, it creates a graphic representation of three statistics: Pearson’s correlation coefficient, root mean square error (RMSE) and standard deviation. In this diagram, the blue contours represent the Pearson correlation coefficient, the black contours on the vertical axis represent the standard deviation, and the green contours on the horizontal axis represent the RMSE values of each model. The distance between the points corresponding to each model with the point named “Score� on the horizontal axis is a measure to check the ability of models to reproduce observations. According to this figure, it can be concluded that the proposed model is closer to the “Score� point. As a result, it has a better performance than others in reproducing its observations. The results of this diagram also emphasize the lower accuracy of ANN(SCG) model compared to others.

The Taylor diagram related to all models.

Full size image

Table 3 presents the results obtained through the experiments, numerically. These results include the values of evaluation indices including RMSE, MAPE, R², PLCC, SROCC and CCC related to all models.

As shown in Table 3, the proposed approach outperforms the “no FS� scenario. This difference can be interpreted as the effectiveness of the proposed feature selection scheme. Additionally, compared to the “LM� and “SCG� cases, the proposed approach obtained superior results. This shows that using CapSA for tuning and training MLPs is a more efficient approach compared to the conventional training algorithms.

The previous section was devoted to the description of the results obtained with the help of the proposed model for estimating the quality of AI education. This section provides a deeper understanding of these findings with focus on the strengths of the proposed approach and its applications. Also, limitations of the study and future works are presented in the continuation of this section.

Discussion of findings and benefits

The findings clearly show that the proposed model is superior to the benchmark models in predicting the quality of AI education. The methodology of using CapSA for feature selection and the adopted MLP architecture was very useful in improving the predictive performance of the model. The results proved the usefulness of employing CapSA in both of its use cases, i.e., feature selection, and MLP tuning. Comparing the proposed method with the case which employes all features for prediction (the “no FS� case) shows at least 4.2% reduction in error percentage. This improvement was evident through all evaluated metrics and proves that the proposed feature selection can reduce the complexity of the prediction problem. Additionally, by comparing the proposed approach with conventional ANN training algorithms (the “LM� and “SCG� cases), the same findings were obtained. This means that using CapSA for tuning the weight of ANN neurons can lead to a more accurate prediction model compared to the conventional LM and SCG training algorithms. However, employing CapSA in both of the mentioned steps leads to an increased computation complexity which may reduce the applicability of the model in various configurations.

On the basis of the results obtained, it can be concluded that the proposed model performed better in terms of minimizing the errors as reflected by the consistently lower values of RMSE and MAPE. The box plots further strengthened this conclusion by providing visual aids that depicted the model’s stability and accuracy. The high R², PLCC, SROCC, and CCC values as well as the Taylor diagram also suggest that the model provides a good fit and performs well in reproducing the underlying data structure and in giving reasonable forecasts.

Feature selection was very important in increasing the accuracy of the model to a significant level. Since the model was able to filter out the most significant factors that impact the quality of AI education, the model’s ability to predict was enhanced. The choice of “Rate of student participation in doing assignments outside of class� and “Average student evaluation score during the academic term� as the key indicators corresponds to the common sense of how these factors influence the learning outcomes.

However, the ANN(SCG) model gave the worst results in all the evaluated measures, thus underlining the need to choose the right model and adjust parameters correctly. As for the other benchmark models, they demonstrated fairly good performance but were surpassed by the proposed approach systematically.

Practical applications

The implication of this study is that the management of higher education institutions aiming at improving the quality of their AI education programs will benefit from the current study. As a result, the proposed model can help to indicate the areas of AI education quality that need improvements or can be considered as successful. In addition, the model can be used to make decisions concerning funding, program content, and faculty professional development based on research. Through identification of these factors, it is possible to focus on the areas that require enhancement on the education of AI so as to bring the necessary change.

It is also possible to use the proposed framework for the purpose of assessing the impact of various instructional and instructional technology strategies and instructional methods in AI education. Thus, tracking the effect of these interventions on the observed quality metric that was predicted allows for making evidence-based decisions about the educational practices in institutions. Thus, the proposed model can be considered as the potential solution for the prediction and enhancement of the quality in AI education. In comparison to the current approaches, its high performance can be explained by the possibilities of applying the environmental analysis and machine learning methodologies. Other developments which can be done in the subsequent studies are the extension of the model to other education settings and the integration of other variables like students’ characteristics and learning preferences into the model.

Limitations and future directions

It is useful to identify some limitations of the proposed model, although it has a high potential. First, the study was based on data gathered from a particular context, which restricts the possibility of comparing results with other educational environments. Secondly, the data set applied in this research included a specific group of indicators that concerned the quality of the AI education. Perhaps, if the number of indicators is increased, it will be possible to obtain a more complete picture of the phenomenon under study. Further, in the proposed model, the main emphasis was made on the prediction of the general AI education quality. Further research may examine the creation of sub-models to capture other facets of AI education like students’ learning, faculty satisfaction, or program efficiency.

Based on the limitations of this research, the following directions for further investigation can be proposed:

• One such area of research concern pertains to the dynamic aspect of AI education quality, where the use of temporal data is needed to study the changes that occur over time. This would help researchers to determine the effect of various interventions and even new trends that may be developing.

• Moreover, it is possible to consider the possibility of using other more sophisticated methods of machine learning, for example, deep learning or reinforcement learning to increase the accuracy of the model and improve its readability. Furthermore, research on the application of the model that integrates two or more machine learning algorithms may provide further advantages.

• Last but not the least, comparative analysis of the proposed model in different educational institutions and countries might help to understand the applicability of the model and the factors that affect the quality of AI education in particular context.

This research presented an approach for predicting the AI education quality. The introduced approach is a three-phase mechanism in which after pre-processing data, a feature selection algorithm based on CapSA is employed for determining the relevant features with the target variable. Finally, a hybrid CapSA-MLP model is used for prediction based on the selected attributes. This approach was examined by real-world data and its efficiency was compared with deep learning and classical ML models in terms of RMSE, MAPE, R², CCC, SROCC, and PLCC. Also, an ablation study was conducted to evaluate the efficiency of each technique employed in the presented approach. According to the experiments, the presented CapSA-based feature selection mechanism could reduce the prediction error by 4.2%. This is while using CapSA for configuring and training the MLP model can reduce the prediction error by at least 1.8% compared to the conventional training algorithms such as LM or SCG. Additionally, comparing the proposed approach with previous algorithms demonstrated 3.9% and 3.3% reduction in prediction error compared to DNN¹⁷ and SVM-based¹⁸ prediction models, respectively.

The proposed approach can be used in any context of education to determine the strengths and the areas of development of the AI education programs, which can be subsequently improved. For instance, teachers can use the model to determine where they require more material or help, and policy makers can use the findings to make sound decisions. Despite the fact that our proposed approach shows certain effectiveness, the further studies are required to consider how the proposed approach can be applied to other educational contexts, and which feature engineering strategies have the positive effect on the model performance. Further, it is also possible to continue the work in the future with the development of more complex hybrid models with the help of more complex deep learning structures and optimization methods.